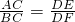题目内容
根据下列条件能判断△ABC和△DEF相似的是( )
| A、∠A=52°,∠B=58°,∠E=58°,∠F=60° | ||||
B、∠C=78°,∠E=78°,
| ||||
| C、∠A=∠F=90°,AC=5,BC=13,FD=10,ED=26 | ||||
| D、AB=1,AC=1.5,BC=2,EF=8,DE=10,FD=16 |
分析:应用两三角形相似的判定定理,对各选项依次判断即可.
解答:解:选项A:∵∠C=180°-∠A-∠B=70°,∠D=180°-∠E-∠F=62°,
∴∠C不等于∠D,∠E,∠F中的任何一个,
∴△ABC和△DEF不相似;
选项B:∵∠C=∠E=78°,要使△ABC∽△DEF,
只需
=
,与已知不符,故不能判断△ABC和△DEF相似;
选项C:∵∠A=∠F=90°,AC=5,BC=13,FD=10,ED=26
∴AC:FD=BC:ED=1:2,
∴△ABC∽△DEF;
选项D:∵AB=1,AC=1.5,BC=2,EF=8,DE=10,FD=16
∴
=
≠
,
即不相似.
故选C.
∴∠C不等于∠D,∠E,∠F中的任何一个,
∴△ABC和△DEF不相似;
选项B:∵∠C=∠E=78°,要使△ABC∽△DEF,
只需
| AC |
| BC |
| ED |
| EF |
选项C:∵∠A=∠F=90°,AC=5,BC=13,FD=10,ED=26
∴AC:FD=BC:ED=1:2,
∴△ABC∽△DEF;
选项D:∵AB=1,AC=1.5,BC=2,EF=8,DE=10,FD=16
∴
| 1 |
| 8 |
| 2 |
| 16 |
| 1.5 |
| 10 |
即不相似.
故选C.
点评:考查相似三角形的判定定理:
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个三角形相似.
(3)三边对应成比例的两个三角形相似.
(1)两角对应相等的两个三角形相似.
(2)两边对应成比例且夹角相等的两个三角形相似.
(3)三边对应成比例的两个三角形相似.

练习册系列答案
相关题目