题目内容
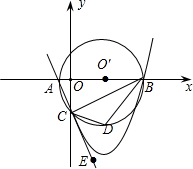 如图所示,已知A点的坐标为(-1,0),点B的坐标是(9,0)以AB为直径作⊙O′,交y轴负半轴于点C,连接AC、BC,过A、B、C作抛物线
如图所示,已知A点的坐标为(-1,0),点B的坐标是(9,0)以AB为直径作⊙O′,交y轴负半轴于点C,连接AC、BC,过A、B、C作抛物线(1)求抛物线的解析式;
(2)点E是AC延长线上的一点,∠BCE的平分线CD交⊙O′于点D,连接BD求BD直线的解析式;
(3)在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的
| 1 | 3 |
分析:(1)根据△OAC∽△OCB即可求得CO的长,即可确定C的坐标,利用待定系数法即可求得抛物线的解析式;
(2)连接O'D,求得D的坐标,再根据待定系数法即可求得直线的解析式;
(3)过点P作PH⊥x轴于H,交直线CD于M,求得直线CD的解析式,即可求得△BCD的面积,然后根据P的横坐标的范围,分情况进行讨论,即可求得.
(2)连接O'D,求得D的坐标,再根据待定系数法即可求得直线的解析式;
(3)过点P作PH⊥x轴于H,交直线CD于M,求得直线CD的解析式,即可求得△BCD的面积,然后根据P的横坐标的范围,分情况进行讨论,即可求得.
解答:解:(1)AB是⊙O'的直径
∴AC⊥BC
又OC⊥AB
∴△OAC∽△OCB
∴
=
∴CO=
=3
∴C(0,-3)(1分)
设抛物线解析式为y=ax2+bx+c,
抛物线过A(-1,0)、B(9,0)和C(0,-3)
∴
解得
(2分)
所求抛物线解析式为y=
x2-
x-3(3分)
(2)连接O'D,
∵CD平分∠BCE,
∴∠BCD=
∠DO'B=45°
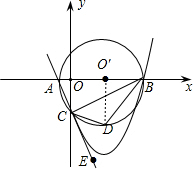 ∴∠DO'B=90°
∴∠DO'B=90°
又DO′=
AB=5
∴D(4,-5)(1分)
设直线BD的解析式为y=kx+b,则
解得
(2分)
直线BD的解析式为y=x-9.(3分)
(3)设点P(x,
x2-
x-3)
过点P作PH⊥x轴于H,交直线CD于M,
易得直线CD的解析式为y=-
x-3,则M(x,-
x-3)
易知直线CD与抛物线交点为C(0,-3)和N(
,-
)
∵S△BCD=S四边形ACDB-S△ABC
=S△AOC+S梯形OCDO'+S△BO′D-S△ABC
+
×4+
-
=15(1分)
设△PCM与△PDM中,边PM上的高分别为h1和h2,则
1当0<x≤42时,如图(1)S△PCD=S△CPM+S△DPM=
(h1+h2)=
[(-
x-3)-(
x2-
x-3)]×4=5
即2x2-13x+15=0
解得x1=
,x2=5>4(舍去)
∴P1(
,-
)(2分)
3当4<x<
时,如图(2)S△PCD=S△CPM-S△DPM=
(h1-h2)=
[(-
x-3)-(
x2-
x-3)]×4=5
即2x2-13x+15=0
解得x1=
<4(舍去),x2=5
∴P2(5,-8)(3分)
5当
<x<96时,如图(3)S△PCD=S△CPM-S△DPM=
(h1-h2)=
[(
x2-
x-3)-(-
x-3)]×4=5
即2x2-13x-15=0
解得x1=
,x2=-1<0(舍去)
∴P3(
,-
)
所有求点P的坐标是P1(
,-
)、P2(5,-8)或P3(
,-
)(4分)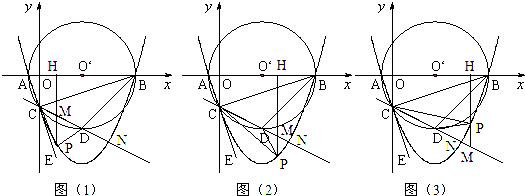
∴AC⊥BC
又OC⊥AB
∴△OAC∽△OCB
∴
| AO |
| CO |
| CO |
| BO |
∴CO=
| AO•BO |
∴C(0,-3)(1分)
设抛物线解析式为y=ax2+bx+c,
抛物线过A(-1,0)、B(9,0)和C(0,-3)
∴
|
|
所求抛物线解析式为y=
| 1 |
| 3 |
| 8 |
| 3 |
(2)连接O'D,
∵CD平分∠BCE,
∴∠BCD=
| 1 |
| 2 |
 ∴∠DO'B=90°
∴∠DO'B=90°又DO′=
| 1 |
| 2 |
∴D(4,-5)(1分)
设直线BD的解析式为y=kx+b,则
|
|
直线BD的解析式为y=x-9.(3分)
(3)设点P(x,
| 1 |
| 3 |
| 8 |
| 3 |
过点P作PH⊥x轴于H,交直线CD于M,
易得直线CD的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
易知直线CD与抛物线交点为C(0,-3)和N(
| 13 |
| 2 |
| 25 |
| 4 |
∵S△BCD=S四边形ACDB-S△ABC
=S△AOC+S梯形OCDO'+S△BO′D-S△ABC
| 1×3 |
| 2 |
| 3+5 |
| 2 |
| 5×5 |
| 2 |
| 10×3 |
| 2 |
设△PCM与△PDM中,边PM上的高分别为h1和h2,则
1当0<x≤42时,如图(1)S△PCD=S△CPM+S△DPM=
| PM |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 8 |
| 3 |
即2x2-13x+15=0
解得x1=
| 3 |
| 2 |
∴P1(
| 3 |
| 2 |
| 25 |
| 4 |
3当4<x<
| 13 |
| 2 |
| PM |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 8 |
| 3 |
即2x2-13x+15=0
解得x1=
| 3 |
| 2 |
∴P2(5,-8)(3分)
5当
| 13 |
| 2 |
| PM |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
即2x2-13x-15=0
解得x1=
| 15 |
| 2 |
∴P3(
| 15 |
| 2 |
| 17 |
| 4 |
所有求点P的坐标是P1(
| 3 |
| 2 |
| 25 |
| 4 |
| 15 |
| 2 |
| 17 |
| 4 |

点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
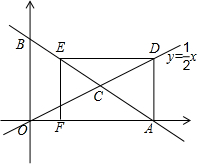 如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线
如图所示,已知A点的坐标为(6,0),B是y轴正半轴上的一动点,直线AB交直线 如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在x轴上.
如图所示,已知A点的坐标为(0,3),⊙A的半径为1,点B在x轴上. 如图所示,已知P点的坐标是(a,b),则sinα等于( )
如图所示,已知P点的坐标是(a,b),则sinα等于( ) 轴上.
轴上.