��Ŀ����
��ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB��4�ף�AC��3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���
�� ����ͼ�ƽ���������ϵ�£����������·�ߵ������߽���ʽ.
�� ����ֱ�ڷ�5��Բ����Ͱʱ��������������Ͱ����˵�����ɣ�
����Ҫʹ����������Ͱ�ڣ�����ֱ�ڷŵ�Բ����Ͱ�ĸ���.
��
 |
��1������������M��0��5����B��2��0����
�������ߵĽ���ʽΪy=ax2+5����B��2��0�������
4a+5=0 ��a=![]()
�������߽���ʽΪ��![]() �� ��������������������������4��
�� ��������������������������4��
��2���ߵ�x=1ʱ��y=![]() ����x=1.5 ʱ��y=
����x=1.5 ʱ��y=![]() ��
��
����ֱ�ڷ�5��Բ����Ͱʱ��Ͱ��=0.3��5=1.5��
��1.5��![]() �� 1.5 ��
�� 1.5 ��![]() ��
��
������������Ͱ�ڣ� ��������������������������8��
��3������ֱ�ڷ�Բ����Ͱm��ʱ�����������Ͱ�ڣ�
������ã� ![]() ��0.3 m��
��0.3 m��![]() ��
��
��ã�![]() ��m��
��m��![]() �� ��˵�������������������δ�ӵ��ں���ɸ��֣�
�� ��˵�������������������δ�ӵ��ں���ɸ��֣�
��mΪ������ ��m��ֵΪ8��9��10��11��12��
�൱��ֱ�ڷ�Բ����Ͱ8��9��10��11��12��ʱ�������������Ͱ�ڣ�������12��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�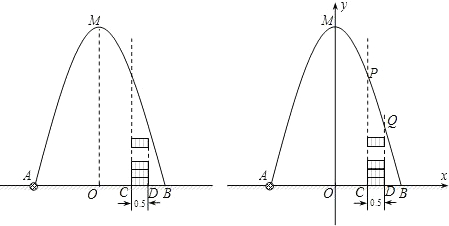
 �������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���
�������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ��� ��ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����AB����ֱ��Ϊx�ᣬOM����ֱ��Ϊy�Ὠ��ƽ��ֱ������ϵ��
��ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��Ϊ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����AB����ֱ��Ϊx�ᣬOM����ֱ��Ϊy�Ὠ��ƽ��ֱ������ϵ�� С��������ķ���������ѧУ��ѧ��¥AB�ĸ߶ȣ���ͼ����ˮƽ�����E����һ��ƽ�澵���������ѧ��¥�ľ���AE=20�ף������뾵�ӵľ���CE=2.5��ʱ�����պ��ܴӾ����п�����ѧ��¥�Ķ���B����֪�����۾������߶�DC=1.6�ף��������С���������¥AB�ĸ߶ȣ�ע�������=����ǣ���
С��������ķ���������ѧУ��ѧ��¥AB�ĸ߶ȣ���ͼ����ˮƽ�����E����һ��ƽ�澵���������ѧ��¥�ľ���AE=20�ף������뾵�ӵľ���CE=2.5��ʱ�����պ��ܴӾ����п�����ѧ��¥�Ķ���B����֪�����۾������߶�DC=1.6�ף��������С���������¥AB�ĸ߶ȣ�ע�������=����ǣ���