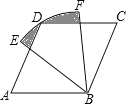
题目内容
【题目】如图,在Rt△ABC中,AB=AC.D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2.
其中正确的是( )

A.②④ B.①④ C.②③ D.①③
【答案】B
【解析】
试题分析:由△ADC绕点A顺时针旋转90°得△AFB,可知△ADC≌△AFB,∠FAD=90°,由∠DAE=45°可判断∠FAE=∠DAE,可证①△AED≌△AEF.由已知条件可证△BEF为直角三角形,则有④BE2+DC2=DE2是正确的.
解:∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,
∴AD=AF,
∵∠DAE=45°,
∴∠FAE=90°﹣∠DAE=45°,
∴∠DAE=∠FAE,AE为△AED和△AEF的公共边,
∴△AED≌△AEF
∴ED=FE
在Rt△ABC中,∠ABC+∠ACB=90°,
又∵∠ACB=∠ABF,
∴∠ABC+∠ABF=90°即∠FBE=90°,
∴在Rt△FBE中BE2+BF2=FE2,
∴BE+DC=DE③显然是不成立的.
故正确的有①④,不正确的有③,②不一定正确.
故选B

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目