题目内容
【题目】 正方形![]() 的边长为1,点
的边长为1,点![]() 是
是![]() 边上的一个动点(与
边上的一个动点(与![]() 不重合),以
不重合),以![]() 为顶点在
为顶点在![]() 所在直线的上方作
所在直线的上方作![]() .
.
(1)当![]() 经过点
经过点![]() 时,
时,
①请直接填空:![]() (可能,不可能)过
(可能,不可能)过![]() 点;(图1仅供分析)
点;(图1仅供分析)
②如图2,在![]() 上截取
上截取![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,册
,册![]() 于
于![]() ,求证:四边形
,求证:四边形![]() 为正方形.
为正方形.
(2)当![]() 不过点
不过点![]() 时,设
时,设![]() 交边
交边![]() 于
于![]() ,且
,且![]() .在
.在![]() 上存在点
上存在点![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,使得
,使得![]() ,连接
,连接![]() ,求四边形
,求四边形![]() 的最大面积.
的最大面积.

【答案】(1)①不可能②证明见解析(2)![]()
【解析】
试题分析:(1)①若ON过点D时,则在△OAD中不满足勾股定理,可知不可能过D点;
②由条件可先判业四边形EFCH为矩形,再证明△OFE≌△ABO,可证得结论;
(2)由条件可证明△PKO∽△OBG,利用相似三角形的性质可求得OP=2,可求得△POG面积为定值及△PKO和△OBG的关系,只要△CGB的面积有最大值时,则四边形PKBG的面积就最大,设OB=a,BG=b,由勾股定理可用b表示出a,则可用a表示出△CBG的面积,利用二次函数的性质可求得其最大值,则可求得四边形PKBG面积的最大值.
试题解析: (1)①若ON过点D,则OA>AB,OD>CD,
∴OA2>AD2,OD2>AD2,
∴OA2+OD2>2AD2≠AD2,
∴∠AOD≠90°,这与∠MON=90°矛盾,
∴ON不可能过D点,
故答案为:不可能;
②∵EH⊥CD,EF⊥BC,
∴∠EHC=∠EFC=90°,且∠HCF=90°,
∴四边形EFCH为矩形,
∵∠MON=90°,
∴∠EOF=90°﹣∠AOB,
在正方形ABCD中,∠BAO=90°﹣∠AOB,
∴∠EOF=∠BAO,
在△OFE和△ABO中
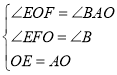
∴△OFE≌△ABO(AAS),
∴EF=OB,OF=AB,
又OF=CF+OC=AB=BC=BO+OC=EF+OC,
∴CF=EF,
∴四边形EFCH为正方形;
(2)∵∠POK=∠OGB,∠PKO=∠OBG,
∴△PKO∽△OBG,
∵S△PKO=4S△OBG,
∴![]() =(
=(![]() )2=4,
)2=4,
∴OP=2,
∴S△POG=![]() OGOP=
OGOP=![]() ×1×2=1,
×1×2=1,

设OB=a,BG=b,则a2+b2=OG2=1,
∴b=![]() ,
,
∴S△OBG=![]() ab=
ab=![]() a
a![]() =
=![]()
![]() =
=![]()
![]() ,
,
∴当a2=![]() 时,△OBG有最大值
时,△OBG有最大值![]() ,此时S△PKO=4S△OBG=1,
,此时S△PKO=4S△OBG=1,
∴四边形PKBG的最大面积为1+1+![]() =
=![]() .
.