题目内容
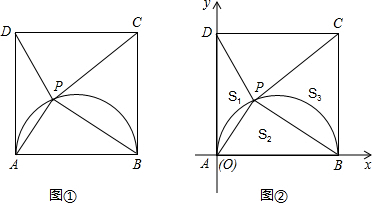
如图,当四边形PABN的周长最小时,a= .
【答案】分析:因为AB,PN的长度都是固定的,所以求出PA+NB的长度就行了.问题就是PA+NB什么时候最短.
把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时PA+NB最短.
设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.
解答: 解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),
解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),
作B′关于x轴的对称点B″,根据作法知点B″(2,1),
设直线AB″的解析式为y=kx+b,
则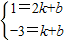 ,解得k=4,b=-7.
,解得k=4,b=-7.
∴y=4x-7.当y=0时,x= ,即P(
,即P( ,0),a=
,0),a= .
.
故答案填: .
.
点评:考查关于X轴的对称点,两点之间线段最短等知识.
把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时PA+NB最短.
设直线AB″的解析式为y=kx+b,待定系数法求直线解析式.即可求得a的值.
解答:
 解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),
解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),
设直线AB″的解析式为y=kx+b,
则
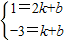 ,解得k=4,b=-7.
,解得k=4,b=-7.∴y=4x-7.当y=0时,x=
 ,即P(
,即P( ,0),a=
,0),a= .
.故答案填:
 .
.点评:考查关于X轴的对称点,两点之间线段最短等知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目