题目内容
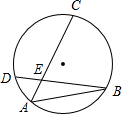 如图,已知AB=BC=CD,弦AC和BD交于点E,∠AED=70°,则∠B=
如图,已知AB=BC=CD,弦AC和BD交于点E,∠AED=70°,则∠B=分析:要求∠B,根据圆周角定理,可转化为求∠DCA,因为AB=BC=CD,所以∠D=∠CBD=∠A=∠ACB,可求∠A=55°,即可求
∠DCA=15°.
∠DCA=15°.
解答: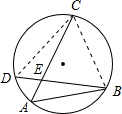 解:连接BC,CD,
解:连接BC,CD,
则有∠DCA=∠DBA,∠D=∠A,
∴DEA=∠DCE+∠D=∠A+∠DBA=70°,
∵AB=BC=CD
∴∠D=∠CBD,∠A=∠ACB,
∴∠ABC=∠CBD+∠DBA=70°,
∴∠A=
=55°,
∴∠DBA=70°-55°=15°.
 解:连接BC,CD,
解:连接BC,CD,则有∠DCA=∠DBA,∠D=∠A,
∴DEA=∠DCE+∠D=∠A+∠DBA=70°,
∵AB=BC=CD
∴∠D=∠CBD,∠A=∠ACB,
∴∠ABC=∠CBD+∠DBA=70°,
∴∠A=
| 180°-70° |
| 2 |
∴∠DBA=70°-55°=15°.
点评:本题考查了:(1)圆周角定理;(2)等边对等角;(3)三角形的外角与内角的关系;(4)三角形内角和定理.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由. 22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.
22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.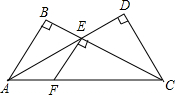 如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有:
如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有: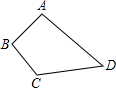 如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为
如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为 如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.
如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.