题目内容
已知 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。

(1)求 的值;
的值;
(2)求直线AB的函数解析式;
(3)若点 ,点
,点 是反比例函数
是反比例函数 图象上的一点,如果以
图象上的一点,如果以 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 的坐标(能求出一个点即可)。
的坐标(能求出一个点即可)。
【答案】
(1)2;(2)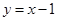 ;(3)D(―2,―1)或(1,2)或
;(3)D(―2,―1)或(1,2)或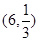
【解析】
试题分析:(1)根据反比例函数图象上的点的坐标的特征求解即可;
(2)先由(1)得到点A、B的坐标,设直线AB的函数解析式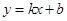 ,根据待定系数法求解即可;
,根据待定系数法求解即可;
(3)连接AB,过点C作AB的平行线交双曲线于点D,则四边形ABDC是梯形,则可得直线CD的函数解析式为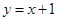 ,由
,由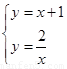 得D(―2,―1)或(1,2);或过点A作CB的平行线交双曲线于点D,则四边形ADBC是梯形。
得D(―2,―1)或(1,2);或过点A作CB的平行线交双曲线于点D,则四边形ADBC是梯形。
这时可求得点D的坐标为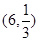 .
.
(1)由已知得,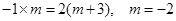
∴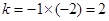 ;
;
(2)由已知得,A(―1,―2),B(2,1)
设直线AB的函数解析式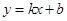 ,
,
则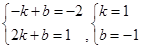
∴直线AB的函数解析式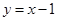 ;
;
(3)连接AB,过点C作AB的平行线交双曲线于点D,则四边形ABDC是梯形
则直线CD的函数解析式为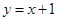 ,
,
由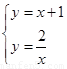 得D(―2,―1)或(1,2)
得D(―2,―1)或(1,2)
或过点A作CB的平行线交双曲线于点D,则四边形ADBC是梯形。
这时可求得点D的坐标为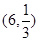 .
.
考点:反比例函数的性质
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
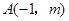 与
与 是反比例函数
是反比例函数 图象上的两个点.
图象上的两个点. 的值;
的值; ,则在反比例函数
,则在反比例函数 ,使得以
,使得以 四点为顶点的四边形为梯形?若存在,求出点
四点为顶点的四边形为梯形?若存在,求出点
 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
 的值;
的值; ,点
,点 是反比例函数
是反比例函数 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
 的值;
的值; ,点
,点 是反比例函数
是反比例函数 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点 与
与 是反比例函数
是反比例函数 图象上的两个点。
图象上的两个点。
 的值;
的值; ,点
,点 是反比例函数
是反比例函数 四点为顶点的四边形为梯形,请你求出点
四点为顶点的四边形为梯形,请你求出点