��Ŀ����
����Ŀ����ͼ���ھ���ABCD�У�AD=acm��AB=bcm��a��b��4�����뾶Ϊ2cm����O�ھ���������AB��AD�����У����ж���P��A��������ھ��α�������A��B��C��D�ķ��������ƶ�������P����D��ʱֹͣ�ƶ�����O�ھ����ڲ���AD��������ƽ�ƣ��ƶ�����CD����ʱ������ԭ·��ԭ�ٷ��أ�����O�ص�����ʱ��λ�ã����ٴ���AB���У�ʱֹͣ�ƶ�����֪��P����Oͬʱ��ʼ�ƶ���ͬʱֹͣ�ƶ�����ͬʱ������Ե���ֹλ�ã���
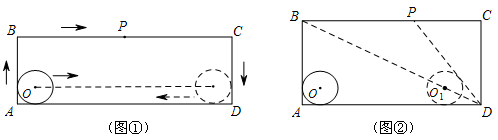
��1����ͼ������P��A��B��C��D��ȫ�̹��ƶ��� cm���ú�a��b�Ĵ���ʽ��ʾ����
��2����ͼ������֪��P��A��������ƶ�2s����B�㣬�����ƶ�3s������BC���е㣮����P����O���ƶ��ٶ���ȣ�������5sʱ����Բ��O�ƶ��ľ��룻
��3����ͼ������֪a=20��b=10���Ƿ�����������Σ�����O������O1��λ��ʱ����ʱԲ��O1�ھ��ζԽ���BD�ϣ���DP����O1ǡ�����У���˵�����ɣ�
���𰸡���1��a+2b����2��20cm����3�����ڣ����ɼ�����.
��������
�����������1����P�˶���·�̵�����AB+BC+CD���ij��ȣ���2��Բ���ƶ��ľ���Ϊ2��a��4��cm��Ȼ����ݵ�P�˶���·�̵���Բ���ƶ��ľ����Լ���P�����ƶ�3s������BC���е㣬����P��3s�ƶ���![]() cm�г�������Ӷ����a��b�ij��ȣ�Ȼ��ó�Բ���ƶ����ٶȣ��Ӷ����Բ���ƶ��ľ��룻��3�����P�ƶ����ٶ�Ϊv1cm/s����O�ƶ����ٶ�Ϊv2cm/s���Ӷ���������ٶȵı�ֵ.��ֱ��OO1��AB���ڵ�E����CD���ڵ�F����O1��AD�����ڵ�G���ó���DO1G�ա�DO1H����BP=xcm����DP=xcm��PC=��20-x��cm������Rt��PCD�Ĺ��ɶ������x��ֵ��������BEO1����BAD�ó�EO1��OO1�ij��ȣ�Ȼ�������O�״ε�����O1��λ��ʱ����O�ƶ��ľ���Ϊ14cm�Լ�����O�ڷ���;�е�����O1��λ��ʱ����O�ƶ��ľ���Ϊ18cm�ֱ����˵�����ó���.
cm�г�������Ӷ����a��b�ij��ȣ�Ȼ��ó�Բ���ƶ����ٶȣ��Ӷ����Բ���ƶ��ľ��룻��3�����P�ƶ����ٶ�Ϊv1cm/s����O�ƶ����ٶ�Ϊv2cm/s���Ӷ���������ٶȵı�ֵ.��ֱ��OO1��AB���ڵ�E����CD���ڵ�F����O1��AD�����ڵ�G���ó���DO1G�ա�DO1H����BP=xcm����DP=xcm��PC=��20-x��cm������Rt��PCD�Ĺ��ɶ������x��ֵ��������BEO1����BAD�ó�EO1��OO1�ij��ȣ�Ȼ�������O�״ε�����O1��λ��ʱ����O�ƶ��ľ���Ϊ14cm�Լ�����O�ڷ���;�е�����O1��λ��ʱ����O�ƶ��ľ���Ϊ18cm�ֱ����˵�����ó���.
�����������1��a+2b��
��2�����������˶������У���P�ƶ��ľ���Ϊ![]() cm��Բ��O�ƶ��ľ���Ϊ
cm��Բ��O�ƶ��ľ���Ϊ![]() cm��
cm��
�����⣬��![]() ��
��
����P�ƶ�2s����B�㣬����P��2s�ƶ���bcm��
��P�����ƶ�3s������BC���е㣬����P��3s�ƶ���![]() cm�� ��
cm�� ��![]() ����
����
���٢����![]() ����P�ƶ����ٶ�����O �ƶ����ٶ���ȣ�
����P�ƶ����ٶ�����O �ƶ����ٶ���ȣ�
����O �ƶ����ٶ�Ϊ![]() ��cm/s���� ����5sʱ����Բ��O�ƶ��ľ���Ϊ5��4=20��cm����
��cm/s���� ����5sʱ����Բ��O�ƶ��ľ���Ϊ5��4=20��cm����
��3��������������
���P�ƶ����ٶ�Ϊv1cm/s����O�ƶ����ٶ�Ϊv2cm/s��
�����⣬��![]() ��
��
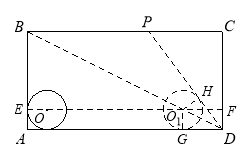
��ͼ����ֱ��OO1��AB���ڵ�E����CD���ڵ�F����O1��AD�����ڵ�G��
��PD����O1�������е�ΪH����O1G=O1H�� ����DO1G�ա�DO1H�����ADB=��BDP��
��BC��AD�����ADB=��CBD�� ���BDP=��CBD����BP=DP�� ��BP=xcm����DP=xcm��PC=��20-x��cm��
��Rt��PCD�����ɹ��ɶ������ɵ�![]() ��
��
��![]() �����
�����![]() ��
��
����ʱ��P�ƶ��ľ���Ϊ![]() ��cm����
��cm����
��EF��AD�����BEO1����BAD��
��![]() ����
����![]() ��
��
��EO1=16cm����OO1=14cm��
������O�״ε�����O1��λ��ʱ����O�ƶ��ľ���Ϊ14cm������ʱ��P����O�ƶ����ٶȱ�Ϊ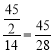 ��
��
��![]() �� ����ʱPD����O1������������
�� ����ʱPD����O1������������
������O�ڷ���;�е�����O1��λ��ʱ����O�ƶ��ľ���Ϊ2����20-4��-14=18��cm����
����ʱ��P����O�ƶ����ٶȱ�Ϊ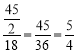 �� ����ʱPD����O1ǡ��������
�� ����ʱPD����O1ǡ��������