题目内容
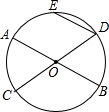 (1998•四川)如图,AB和CD是⊙O的两条直径,弦DE∥AB,弧DE为50°的弧,那么∠BOC为( )
(1998•四川)如图,AB和CD是⊙O的两条直径,弦DE∥AB,弧DE为50°的弧,那么∠BOC为( )分析:连接OE,根据弧DE为50°,求出∠EOD=50°,根据OE=OD,求出∠OED=∠ODE=65°,根据DE∥AB,求出∠AOE=∠OED=65°,∠AOD=∠AOE+∠EOD=65°+50°=115°,最后根据∠BOC=∠AOD即可求出答案.
解答: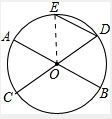 解:连接OE,
解:连接OE,
∵弧DE为50°,
∴∠EOD=50°,
∴∠OED+∠ODE=130°
∵OE=OD,
∴∠OED=∠ODE=65°,
∵DE∥AB,
∴∠AOE=∠OED=65°,
∴∠AOD=∠AOE+∠EOD=65°+50°=115°,
∴∠BOC=∠AOD=115°.
故选A.
 解:连接OE,
解:连接OE,∵弧DE为50°,
∴∠EOD=50°,
∴∠OED+∠ODE=130°
∵OE=OD,
∴∠OED=∠ODE=65°,
∵DE∥AB,
∴∠AOE=∠OED=65°,
∴∠AOD=∠AOE+∠EOD=65°+50°=115°,
∴∠BOC=∠AOD=115°.
故选A.
点评:此题考查了圆心角、弦、弧之间的关系,用到的知识点是圆心角、弦、弧之间的关系、平行线的性质、等腰三角形的性质,关键是做出辅助线,求出∠AOD的度数.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,
(1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M, (1998•四川)已知:如图,∠BAD=∠CAD,AB=AC,点E、A、D在同一条直线上.求证:△ABE≌△ACE.
(1998•四川)已知:如图,∠BAD=∠CAD,AB=AC,点E、A、D在同一条直线上.求证:△ABE≌△ACE. (1998•四川)已知:如图,在以O 为圆心的两个同心圆中,大圆O的内接四边形ABCD的边AB切小圆O于点P,两条对角线AC、BD相交于点Q,AQ和AD的长是方程x2-7x+12=0的两根,小圆O的半径等于CD长的一半,AK是大圆的直径.
(1998•四川)已知:如图,在以O 为圆心的两个同心圆中,大圆O的内接四边形ABCD的边AB切小圆O于点P,两条对角线AC、BD相交于点Q,AQ和AD的长是方程x2-7x+12=0的两根,小圆O的半径等于CD长的一半,AK是大圆的直径.