题目内容
【题目】已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE。
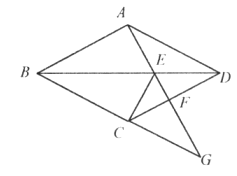
(1)求证:∠DAE=∠DCE; (2)求证:AE2=EF·EG。
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据菱形的性质得出△ADE和△CDE全等,从而得出答案;(2)、根据菱形的性质得出∠DAG=∠G,根据已知条件得出∠DCE=∠G,从而得出△ECF和△EGC相似,结合△ADE和△CDE得出答案.
试题解析:(1)、∵四边形ABCD是菱形 ![]() ,AB∥CD ∴∠ABD=∠ADB,∠ABD=∠CDE,
,AB∥CD ∴∠ABD=∠ADB,∠ABD=∠CDE,
∴∠ADE=∠CDE,AD=CD ![]() ∴△ADE≌△CDE(SAS) ∴∠DAE=∠DCE
∴△ADE≌△CDE(SAS) ∴∠DAE=∠DCE
(2)、∵四边形ABCD是菱形 ∴AD∥BC,∠DAG=∠G ∵∠DAE=∠DCE ∴∠DCE=∠G
∵∠CEF=∠GEC ∴△ECF∽△EGC ![]() ∵△ADE≌△CDE,
∵△ADE≌△CDE,![]()
![]()

练习册系列答案
相关题目
