题目内容
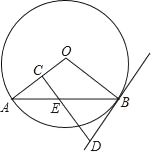
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由切线性质及等量代换推出∠4=∠5,再利用等角对等边可得出结论;
(2)由已知条件得出sin∠DEF和sin∠AOE的值,利用对应角的三角函数值相等推出结论.
试题解析:(1)∵DC⊥OA, ∴∠1+∠3=90°, ∵BD为切线,∴OB⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2,∵∠3=∠4,∴∠4=∠5,在△DEB中, ∠4=∠5,∴DE=DB.
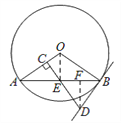
(2)作DF⊥AB于F,连接OE,∵DB=DE, ∴EF=![]() BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=
BE=3,在 RT△DEF中,EF=3,DE=BD=5,EF=3 , ∴DF=![]() ∴sin∠DEF=
∴sin∠DEF=![]() =
= ![]() , ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=
, ∵∠AOE=∠DEF, ∴在RT△AOE中,sin∠AOE=![]() ,
,
∵AE=6, ∴AO=![]() .
.

练习册系列答案
相关题目