Question

【题目】如图，△ABC中，∠ACB=90°，AC=5，BC=12，CO⊥AB于点O，D是线段OB上一点，DE=2，ED∥AC（∠ADE＜90°），连接BE、CD．设BE、CD的中点分别为P、Q．
（1）求AO的长；
（2）求PQ的长；
（3）设PQ与AB的交点为M，请直接写出|PM﹣MQ|的值．

Answer 1

【答案】
（1）解：如图1中，

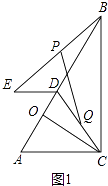
∵CO⊥AB，

∴∠AOC=∠ACB=90°，∵∠A=∠A，

∴△ABC∽△ACO，

∴ = ，

∵AB= = =13，

∴OA= =

（2）解：如图2中，取BD中点F，CD中点Q，连接PF、QF，

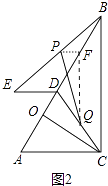
则PF∥ED，FQ∥BC，PF⊥FQ，且PF= ED=1，FQ= BC=6，

在Rt△PFQ中，PQ= = =

（3）解：如图3中，取AD中点G，连接GQ，

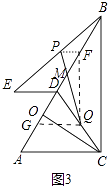
∵GQ∥AC，ED∥AC，PF∥ED，

∴PF∥GQ，

∴△PMF∽△QMG，

∴ = = ，

∵PM+QM= ，

∴PM= ，MQ= ，

∴|PM﹣QM|=

【解析】（1）由△ABC∽△ACO，得 = ，由此即可求出OA．（2）如图2中，取BD中点F，CD中点Q，连接PF、QF，在Rt△PFQ中，求出PF，QF即可解决问题．（3）如图3中，取AD中点G，连接GQ，由PF∥GQ，推出△PMF∽△QMG，推出 = = ，由PM+QM= ，可以求出PM，QM，即可解决问题．