题目内容
【题目】已知抛物线交x轴于A,B两点(A在B右边),A(3,0),B(1,0)交y轴于C点,C(0,3),连接AC;
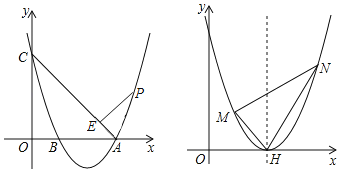
(1)求抛物线的解析式;
(2)P为抛物线上的一点,作PE⊥CA于E点,且CE=3PE,求P点坐标;
(3)将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,过H作直线MH,NH,当MH⊥NH时,求MN恒过的定点坐标.
【答案】(1)y=x2﹣4x+3;(2)(2,﹣1)或(![]() ,
,![]() );(3)MN恒过的定点(2,1)
);(3)MN恒过的定点(2,1)
【解析】
(1)用待定系数解答便可;
(2)分两种情况:P点AC的上方,点P在AC的下方.过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,与PD交于点G,证明EF=3EG,设EG=m,用m的代数式表示P点的横纵坐标,再代入二次函数解析式,便可求得m的值,进而得P点的坐标;
(3)过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,先求出H点的坐标与新抛物线的解析式,设出M、N的坐标,得出两坐标的联系,表示出MN的解析式,再代入定点(2,1)的坐标进行验证便可得解.
(1)∵抛物线过A(3,0),B(1,0),
∴可设抛物线的解析式为y=a(x﹣3)(x﹣1)(a≠0),
把c(0,3)代入,得3a=3,
∴a=1,
∴抛物线的解析式是y=(x﹣3)(x﹣1)=x2﹣4x+3,
即y=x2﹣4x+3;
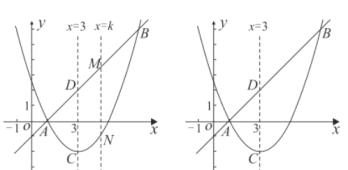
(2)当P点在AC上方时,过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,如图1,

∵A(3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=45°,
∵FG∥OA,
∴∠CEF=45°,
∴CF=EF=![]() CE,
CE,
∵PE⊥CA,
∴∠PEG=45°,
∴PG=EG=![]() PE,
PE,
∵CE=3PE,
∴EF=3FG,
设EF=3m,则PG=EG=m,FG=4m,
∴DG=OF=OC﹣CF=3﹣3m,
PD=PG+DG=3﹣2m,
∴P(4m,3﹣2m),
把P(4m,3﹣2m)代入y=x2﹣4x+3中得,
3﹣2m=16m2﹣16m+3,
∴m=![]() ,或m=0(舍去),
,或m=0(舍去),
∴P(![]() ,
,![]() );
);
当P点AC下方时,如图2,过点P作PD⊥x轴于点D,过E作EF⊥y轴于F,延长FE与PD交于点G,
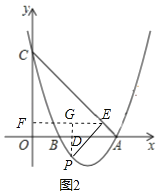
∵A(3,0),C(0,3),
∴OA=OC=3,
∴∠OAC=45°,
∵FE∥OA,
∴∠CEF=45°,
∴CF=EF=![]() CE,
CE,
∵PE⊥CA,
∴∠PEG=45°,
∴PG=EG=![]() PE,
PE,
∵CE=3PE,
∴EF=3FG,
设EF=3m,则PG=EG=m,EG=2m,
∴DG=OF=OC﹣CF=3﹣3m,
PD=PG﹣DG=4m﹣3,
∴P(2m,3﹣4m),
把P(2m,3﹣4m)代入y=x2﹣4x+3中得,
3﹣4m=4m2﹣8m+3,
∴m=1,或m=0(舍去),
∴P(2,﹣1);
综上,P点的坐标为(2,﹣1)或(![]() ,
,![]() );
);
(3)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线y=x2﹣4x+3的顶点为(2,﹣1),
∵将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,
∴H(2,0),
由题意知,点H是新抛物线的顶点,
∴新抛物线的解析式为y=(x﹣2)2,
设M(m,(m﹣2)2),N(n,(n﹣2)2),
过M作MK⊥x轴于点K,过点N作NL⊥x轴于点L,如图3,

则MK=(m﹣2)2,KH=2﹣m,HL=n﹣2,NL=(n﹣2)2,
∵MH⊥NH,
∴∠MHK+∠HMK=∠MHK+∠NHL=90°,
∴∠HMK=∠NHL,
∵∠MKH=∠HLN=90°,
∴△KHM∽△LNH,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
设直线MN的解析式为:y=kx+b(k≠0),则 ,
,
∴ ,
,
∴直线MN的解析式为:![]() ,
,
当x=2时,![]() =(m-2)2﹣(m2﹣4m+3)
=(m-2)2﹣(m2﹣4m+3)
=m2﹣4m+4﹣m2+4m﹣3=1,
∴MN恒过的定点(2,1).

【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
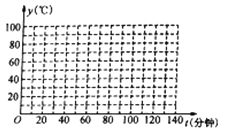
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?