Question

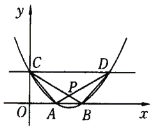
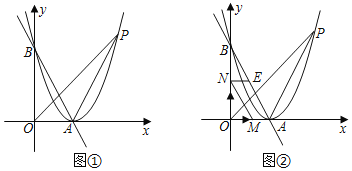
【题目】如图①，直线y＝﹣x+2与x轴，y轴分别交于A，B两点，以A为顶点的抛物线经过点B，点P是抛物线上一点，连接OP，AP．

（1）求抛物线的解析式；

（2）若△AOP的面积是3，求P点坐标；

（3）如图②，动点M，N同时从点O出发，点M以1个单位长度/秒的速度沿x轴正半轴方向匀速运动，点N以个单位长度/秒的速度沿y轴正半轴方向匀速运动，当其中一个动点停止运动时，另一个动点也随之停止运动，过点N作NE∥x轴交直线AB于点E．若设运动时间为t秒，是否存在某一时刻，使四边形AMNE是菱形？若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）抛物线的表达式为：y＝x2﹣2x+2；（2）点P的坐标为：（2+，3）或（2﹣，3）；（3）存在t＝，理由见解析．

【解析】

（1）求出点A、B的坐标；因为抛物线的顶点为点A，所以设抛物线的表达式为：y=a（x-2）2，将点B的坐标代入上式，即可求解；
（2）△AOP的面积=×OA×yP=×2×yP=3，解得：yP=3，即可求解；
（3）t秒时，点M、N的坐标分别为：（t，0）、（0，t），则点E（2-t，t），而点N（0，t），故NE=2-t，当四边形AMNE是菱形时，NE=MN，即可求解．

（1）y＝﹣x+2，令x＝0，则y＝2，令y＝0，则x＝2，

故点A、B的坐标分别为：（2，0）、（0，2），

∵抛物线的顶点为点A（2，0），

∴设抛物线的表达式为：y＝a（x﹣2）2，

将点B的坐标代入上式得：2＝a（0﹣2）2，解得：a＝，

故抛物线的表达式为：y＝（x﹣2）2＝x2﹣2x+2；

（2）∵点A（2，0），则OA＝2，

∴△AOP的面积＝×OA×yP＝2×yP＝3，

解得：yP＝3，

则yP＝3＝（x﹣2）2，解得：x＝2，

故点P的坐标为：（2+，3）或（2﹣，3）；

（3）存在，理由：

由题意得：t秒时，点M、N的坐标分别为：（t，0）、（0，t），

当y＝t时，y＝t＝﹣x+2，解得：x＝2﹣t，故点E（2﹣t，t），

而点N（0，t），故NE＝2﹣t，

当四边形AMNE是菱形时，NE＝MN，

即t2+（t）2＝（2﹣t）2，

解得：t＝或﹣2（舍去﹣2），

故t＝．