Question

【题目】如图，直线y＝x+b与y轴交于点A（0，4），与函数y＝（k＞0，x＜0）的图象交于点C，以AC为对角线作矩形ABCD，使顶点B，D落在x轴上（点D在点B的右边），BD与AC交于点E．

（1）求b和k的值；

（2）求顶点B，D的坐标．

Answer 1

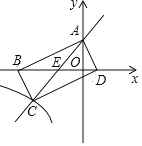
【答案】（1）4，24；（2）B(﹣8，0)，D(2，0)

【解析】

（1）根据点A坐标可以确定b的值，得出直线的解析式，令y＝0，求得E的坐标，由E（﹣3，0）是AC的中点，推出点C（﹣6，﹣4），然后根据待定系数法即可求得k；

（2）根据勾股定理求得AE，利用矩形的性质EA＝EB＝ED，即可解决问题；

解：（1）∵直线y＝x+b与y轴交于点A（0，4），

∴b＝4，

∴直线为y＝x+4，

令y＝0，解得x＝﹣3，

∴E（﹣3，0），

∵四边形ABCD是矩形，

∴E（﹣3，0）是AC的中点，

∴C（﹣6，﹣4），

∵点C在函数y＝的图象上，

∴k＝﹣6×（﹣4）＝24；

（2）∵AE2＝AO2+EO2，

∴AE＝＝5，

∵四边形ABCD是矩形，

∴ED＝EB＝EA＝5，

∴B（﹣8，0），D（2，0）．