题目内容
 如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
(1)判断四边形ABDE的形状,并说明理由;
(2)问:线段CE与线段AD有什么关系?请说明你的理由.
(1)解:四边形ABDE是平行四边形,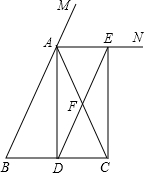
理由如下:
∵AB=AC,D是BC中点,F是AC中点,
∴DF∥AB,
∵AB=AC,D是BC中点,
∴∠BAD=∠CAD,AD⊥DC,
∵AN是△ABC的外角∠MAC的角平分线,
∴∠MAE=∠CAE,
∴∠NAD=90°,
∴AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:CE∥AD,CE=AD;
理由如下:
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE= ∠MAC,
∠MAC,
∵∠MAC=∠B+∠ACB,
∵AB=AC,∴∠B=∠ACB,
∴∠MAE=∠B,∴AN∥BC,
∵AB=AC,点D为BC中点,∴AD⊥BC,
∵CE⊥AN,∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形)
∴CE∥AD,CE=AD.
分析:(1)四边形ABDE是平行四边形,有等腰三角形的性质和中位线的性质可证明:AB∥DE,再利用等腰三角形的性质和角平分线的定义证明AE∥BD,进而证明四边形ABDE的形状为平行四边形;
(2)CE∥AD,CE=AD;证明四边形ADCE为矩形即可;
点评:本题的考点:外角的性质,等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】)平行四边形和矩形的判定和性质.

理由如下:
∵AB=AC,D是BC中点,F是AC中点,
∴DF∥AB,
∵AB=AC,D是BC中点,
∴∠BAD=∠CAD,AD⊥DC,
∵AN是△ABC的外角∠MAC的角平分线,
∴∠MAE=∠CAE,
∴∠NAD=90°,
∴AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:CE∥AD,CE=AD;
理由如下:
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=
 ∠MAC,
∠MAC,∵∠MAC=∠B+∠ACB,
∵AB=AC,∴∠B=∠ACB,
∴∠MAE=∠B,∴AN∥BC,
∵AB=AC,点D为BC中点,∴AD⊥BC,
∵CE⊥AN,∴AD∥CE,
∴四边形ADCE为平行四边形(有两组对边分别平行的四边形是平行四边形),
∵CE⊥AN,∴∠AEC=90°,
∴四边形ADCE为矩形(有一个角是直角的平行四边形是矩形)
∴CE∥AD,CE=AD.
分析:(1)四边形ABDE是平行四边形,有等腰三角形的性质和中位线的性质可证明:AB∥DE,再利用等腰三角形的性质和角平分线的定义证明AE∥BD,进而证明四边形ABDE的形状为平行四边形;
(2)CE∥AD,CE=AD;证明四边形ADCE为矩形即可;
点评:本题的考点:外角的性质,等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.【三线合一】)平行四边形和矩形的判定和性质.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
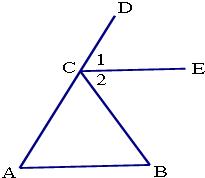 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.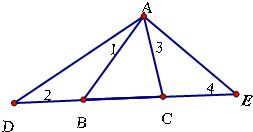 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )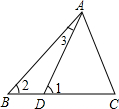 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.