题目内容
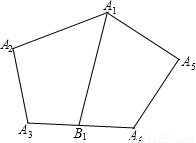
（2003•安徽）附加题：如图，在五边形A1A2A3A4A5中，B1是A1对边A3A4的中点，连接A1B1，我们称A1B1是这个五边形的一条中对线．如果五边形的每条中对线都将五边形的面积分成相等的两部分．求证：五边形的每条边都有一条对角线和它平行．
【答案】分析：可以再做五边形的一条中对线，根据它们分割成的两部分的面积相等，都是五边形的面积的一半，导出两个等底的三角形的面积相等，从而得到它们的高相等，则得到五边形的每条边都有一条对角线和它平行．
解答：证明：取A1A5中点B3，连接A3B3、A1A3、A1A4、A3A5，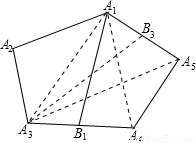
∵A3B1=B1A4，
∴S△A1A3B1=S△A1B1A4，
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等，
∴S△A1A2A3=S△A1A4A5，
同理S△A1A2A3=S△A3A4A5，
∴S△A1A4A5=S△A3A4A5，
∴△A3A4A5与△A1A4A5边A4A5上的高相等，
∴A1A3∥A4A5，
同理可证A1A2∥A3A5，A2A3∥A1A4，A3A4∥A2A5，A5A1∥A2A4．
点评：此题要能够根据面积相等得到两条直线间的距离相等，从而证明两条直线平行．
解答：证明：取A1A5中点B3，连接A3B3、A1A3、A1A4、A3A5，
∵A3B1=B1A4，
∴S△A1A3B1=S△A1B1A4，
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等，
∴S△A1A2A3=S△A1A4A5，
同理S△A1A2A3=S△A3A4A5，
∴S△A1A4A5=S△A3A4A5，
∴△A3A4A5与△A1A4A5边A4A5上的高相等，
∴A1A3∥A4A5，
同理可证A1A2∥A3A5，A2A3∥A1A4，A3A4∥A2A5，A5A1∥A2A4．
点评：此题要能够根据面积相等得到两条直线间的距离相等，从而证明两条直线平行．
练习册系列答案
相关题目
