题目内容
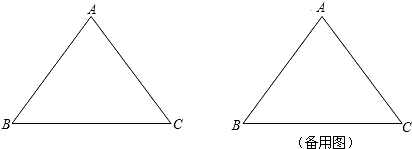
在等腰△ABC中,已知AB=AC=5cm,BC=6cm,动点P、Q分别从A、B两点同时出发,沿AB、BC方向匀速移动,它们的速度都是1 cm/秒.当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(秒).
(1)当t为何值时,PQ⊥AB?
(2)设四边形APQC的面积为ycm2,写出y关于t的函数关系式及定义域;
(3)分别以P、Q为圆心,PA、BQ长为半径画圆,若⊙P与⊙Q相切,求t的值;
(4)在P、Q运动中,△BPQ与△ABC能否相似?若能,请求出AP的长;若不能,请说明理由.
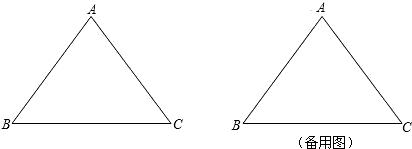
 解:(1)过A作AH⊥BC,垂足为H,
解:(1)过A作AH⊥BC,垂足为H,∵AB=AC,AH⊥BC,
∴BH=
 BC=3.
BC=3.又∵PQ⊥AB,
∴cos∠B=
 .
.∴
 .
.∴t=
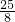 .
.(2)过P作PM⊥BC,垂足为M,
∵PM⊥BCAH⊥BC,
∴PM∥AH.
∴
 .
.∴
 .
.∴PM=
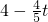 .
.∴S△PBQ=
 .
.∴
 .
.∴定义域:0<t<5.
(3)∵PA=BQ=t,
∴两圆只能外切.
过Q作QN⊥AB,垂足为N,
∵sin∠B=
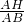 =
= ,
,在Rt△BNQ中,
∴QN=
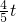 ,BN=
,BN=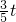 ,PN=
,PN= .
.又∵∠PNQ=90°,
∴
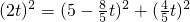 .
.∴t=-10+

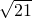 ;
;
(4)能,有二种情况:
①∵△BPQ∽△BAC,
∴
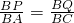 .
.∴
 .
.∴t=
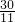 .
.②∵△BPQ∽△BCA,
∴
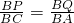 .
.∴
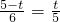 .
.∴t=
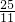 .
.∴当t=
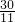 或t=
或t=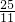 秒时,两个三角形相似.
秒时,两个三角形相似.分析:(1)过A作AH⊥BC,垂足为H,根据三角函数cos∠B得出等量关系,求出t的值;
(2)等量关系S四边形APQC=S△ABC-S△BPQ得出y关于t的函数关系式及定义域;
(3)以P、Q为圆心,PA、BQ长为半径画圆,若⊙P与⊙Q相切,两圆只能外切,根据圆与圆的外切位置关系,求t的值;
(4)△BPQ与△ABC相似,∠B公共,∠A=∠BPQ,或∠A=∠BQP,得出AP的长.
点评:本题综合考查了直线与圆、圆与圆的位置关系,相似三角形的判定和性质,是一个探究性性的题目,一定要分析各种情况,不要落漏.

练习册系列答案
相关题目
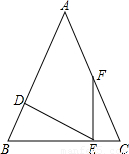
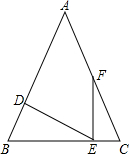 E作EF⊥BC交AC边于点F.
E作EF⊥BC交AC边于点F.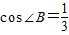 ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.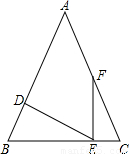
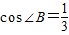 ,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.
,D为AB上一点,过点D作DE⊥AB交BC边于点E,过点E作EF⊥BC交AC边于点F.