题目内容
(2013•大庆模拟)甲乙两地相距400km,一辆轿车从甲地出发,以80km/h的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地.货车出发2.5h后与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.设轿车行驶的时间为x(h),两车距乙地的距离为y(km).
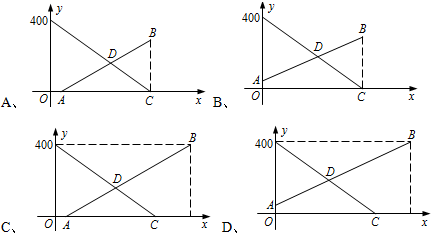
(1)两车距乙地的距离与x之间的函数关系,在同一坐标系中画出的图象是
(2)求货车距乙地的距离y1与x之间的函数关系式.
(3)在甲乙两地间,距乙地300km处有一个加油站,两车在行驶过程中都曾在该加油站加油(加油时间忽略不计).求两车加油的间隔时间是多少?

(1)两车距乙地的距离与x之间的函数关系,在同一坐标系中画出的图象是
C
C
(2)求货车距乙地的距离y1与x之间的函数关系式.
(3)在甲乙两地间,距乙地300km处有一个加油站,两车在行驶过程中都曾在该加油站加油(加油时间忽略不计).求两车加油的间隔时间是多少?
分析:(1)根据货车晚出发0.5小时,与x轴的交点为(0.5,0),货车最后到达甲地,y值为400,判断出C选项图形符合;
(2)根据时间=路程÷速度求出轿车到达乙地的时间,然后求出轿车的函数解析式,再求出相遇点D的坐标,再利用待定系数法求出货车函数解析式;
(3)根据轿车与货车的函数解析式,分别求出进站加油的时间,然后相减即可得到间隔时间.
(2)根据时间=路程÷速度求出轿车到达乙地的时间,然后求出轿车的函数解析式,再求出相遇点D的坐标,再利用待定系数法求出货车函数解析式;
(3)根据轿车与货车的函数解析式,分别求出进站加油的时间,然后相减即可得到间隔时间.
解答:解:(1)∵轿车出发0.5h后货车出发,
∴点A的坐标为(0.5,0),
又∵货车最后到达甲地,
∴点B的纵坐标为400,
纵观各选项,只有C符合,
故选C;
(2)轿车行驶时间为400÷80=5(h),
设轿车离乙地距离为y2,y2=k2x+b2,
代入(0,400),(5,0)得,
,
解得
,
∴y2=-80x+400,
代入x=3得,y=160,
即D点坐标为(3,160),
设y1=k1x+b1,
代入A(0.5,0)、D(3,160)得,
,
解得
,
所以,y1=64x-32;
(3)将y1=300代入y1=64x-32得,x1=
,
将y2=300代入y2=-80x+400得,x2=
,
所以,x1-x2=
.
答:两车加油的间隔时间是
h.
∴点A的坐标为(0.5,0),
又∵货车最后到达甲地,
∴点B的纵坐标为400,
纵观各选项,只有C符合,
故选C;
(2)轿车行驶时间为400÷80=5(h),
设轿车离乙地距离为y2,y2=k2x+b2,
代入(0,400),(5,0)得,
|
解得
|
∴y2=-80x+400,
代入x=3得,y=160,
即D点坐标为(3,160),
设y1=k1x+b1,
代入A(0.5,0)、D(3,160)得,
|
解得
|
所以,y1=64x-32;
(3)将y1=300代入y1=64x-32得,x1=
| 83 |
| 16 |
将y2=300代入y2=-80x+400得,x2=
| 5 |
| 4 |
所以,x1-x2=
| 63 |
| 16 |
答:两车加油的间隔时间是
| 63 |
| 16 |
点评:本题考查了一次函数的应用,主要涉及时间、速度、路程三者之间的关系,待定系数法求一次函数解析式,以及已知函数值求自变量,难度不是很大,仔细分析两车行驶过程便不难求解.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
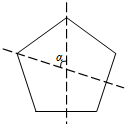 (2013•大庆模拟)已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线.如图所示的正五边形中相邻两条对称轴所夹锐角α的度数为( )
(2013•大庆模拟)已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线.如图所示的正五边形中相邻两条对称轴所夹锐角α的度数为( )