题目内容
设直线kx+(k+1)y=1(k为自然数)与两坐标轴所围成的图形的面积为Sk(k=1,2,3,…,2000).则S1+S2+S3+…+S2000=
.
| 1000 |
| 2001 |
| 1000 |
| 2001 |
分析:画出函数的草图,求出直线与两坐标轴的交点,再求出围成的图形的面积.
解答: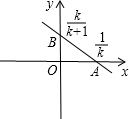 解:如图:直线kx+(k+1)y=1(k为正整数),与x轴的交点坐标为(
解:如图:直线kx+(k+1)y=1(k为正整数),与x轴的交点坐标为(
,0),与y轴的交点坐标为(0,
).
则S△ABO=
×
×
,
S1=
;
S2=
,
…
S2000=
,
S1+S2+S3+…+S2000=
+
+…+
=
(
+
+…+
)
=
(1-
+
-
+
-
+…
-
)
=
.
故答案为:
.
 解:如图:直线kx+(k+1)y=1(k为正整数),与x轴的交点坐标为(
解:如图:直线kx+(k+1)y=1(k为正整数),与x轴的交点坐标为(| 1 |
| k |
| 1 |
| k+1 |
则S△ABO=
| 1 |
| 2 |
| 1 |
| k |
| 1 |
| k+1 |
S1=
| 1 |
| 2×2 |
S2=
| 1 |
| 2×2×3 |
…
S2000=
| 1 |
| 2×2000×2001 |
S1+S2+S3+…+S2000=
| 1 |
| 2×2 |
| 1 |
| 2×2×3 |
| 1 |
| 2×2000×2001 |
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2000×2001 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2000 |
| 1 |
| 2001 |
=
| 1000 |
| 2001 |
故答案为:
| 1000 |
| 2001 |
点评:本题考查的是一次函数图象上点的坐标特点,根据题意找出规律是解答此题的关键.

练习册系列答案
相关题目