题目内容
如图，已知AD是三角形ABC的角∠BAC的角平分线，DF垂直AB于F，DE垂直AC于E，求证：AE=AF，AD平分∠EDF．分析：由AD是三角形ABC的角∠BAC的角平分线，DF垂直AB于F，DE垂直AC于E，由三角形内角和定理，易求得∠ADE=∠ADF，即AD平分∠EDF，然后由角平分线的性质，可证得AE=AF．
解答：证明：∵DF⊥AB，DE⊥AC，
∴∠AFD=∠AED=90°，
∵AD是∠BAC的角平分线，
∴∠EAD=∠FAD，
∵∠EAD+∠AED+∠ADE=180°，∠DAF+∠AFD+∠ADF=180°，
∴∠ADE=∠ADF，
即AD平分∠EDF，
∴AE=AF．
∴∠AFD=∠AED=90°，
∵AD是∠BAC的角平分线，
∴∠EAD=∠FAD，
∵∠EAD+∠AED+∠ADE=180°，∠DAF+∠AFD+∠ADF=180°，
∴∠ADE=∠ADF，
即AD平分∠EDF，
∴AE=AF．
点评：此题考查了角平分线的性质以及三角形内角和定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
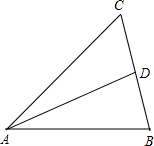如图，已知AD是△ABC的中线．
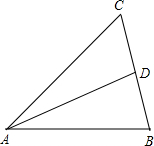如图，已知AD是△ABC的中线．