题目内容
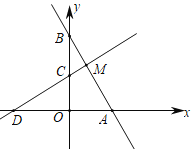
【题目】在平面直角坐标系中,已知直线l:y=﹣![]() x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
(1)写出S与m之间的函数表达式,并写出m的取值范围.
(2)当S=3时,求点P的坐标.
(3)若直线OP平分△AOB的面积,求点P的坐标.
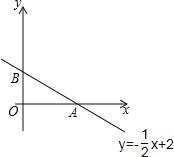
【答案】(1)S=4﹣m,0<m<4;(2)(1,![]() );(3)(2,1)
);(3)(2,1)
【解析】
(1)根据点A、P的坐标求得△AOP的底边与高线的长度;然后根据三角形的面积公式即可求得S与m的函数关系式;
(2)将S=3代入(1)中所求的式子,即可求出点P的坐标;
(3)由直线OP平分△AOB的面积,可知OP为△AOB的中线,点P为AB的中点,根据中点坐标公式即可求解.
解:∵直线l:y=﹣![]() x+2交x轴于点A,交y轴于点B,
x+2交x轴于点A,交y轴于点B,
∴A(4,0),B(0,2),
∵P(m,n)
∴S=![]() ×4×
×4×![]() (4﹣m)=4﹣m,即S=4﹣m.
(4﹣m)=4﹣m,即S=4﹣m.
∵点P(m,n)在第一象限内,∴m+2n=4,
∴ ,
,
解得0<m<4;
(2)当S=3时,4﹣m=3,
解得m=1,
此时y=![]() (4﹣1)=
(4﹣1)=![]() ,
,
故点P的坐标为(1,![]() );
);
(3)若直线OP平分△AOB的面积,则点P为AB的中点.
∵A(4,0),B(0,2),
∴点P的坐标为(2,1).

练习册系列答案
相关题目