题目内容
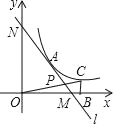
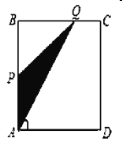
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的高,
边上的高,![]() ,两边分别交
,两边分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,则
,则![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
通过过D作DM⊥AC,DN⊥BC,构造△DME∽△DNF,得对应边成比例,再证明△ACB∽△CND得对应边成比例,结合两个比例式求线段的比.
解:如图,过D作DM⊥AC,DN⊥BC,垂足为M,N,则∠DMC=∠DNC=∠ACB=90°,
∴四边形DMCN是矩形,
∴DM=CN.
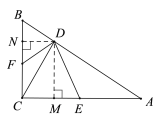
在Rt△ACB中,AB=5,AC=4,由勾股定理得,BC=3,
∵∠BCD=∠A=90°-∠ACD,∠ACB=∠CND=90°,
∴△ACB∽△CND,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠EDM=∠FDN=90°-∠FDM,∠DME=∠DNF=90°,
∴△DME∽△DNF,
∴![]() .
.
即DE:DF=4:3
故选:B

练习册系列答案
相关题目