题目内容
如图有两个转盘，每个转盘都分为3个相同大小的扇形区域，分别用序号1，2，3标出．现转动两个转盘，等转盘停止转动时，指针指向每个区域的可能性相等（不计指针与两个区域交线重合的情形），将所得区域的序号相乘，比较所得积为奇数和偶数的概率的大小．有人说：因为两个转盘中奇数序号比偶数序号多，显然所得积为奇数的概率大，你同意他的说法吗？请说明理由．
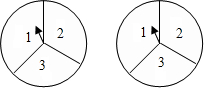
不同意．
（树状图或列表正确）
由树状图（或列表）可知，共有9种等可能结果，
其中积为奇数的有4种，积为偶数的有5种，
∴积为奇数的概率=
，
积为偶数的概率=
，
∴积为偶数的概率大，所以不同意．
（树状图或列表正确）
| 积 一 二 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 |
| 2 | 2 | 4 | 6 |
| 3 | 3 | 6 | 9 |
其中积为奇数的有4种，积为偶数的有5种，
∴积为奇数的概率=
| 4 |
| 9 |
积为偶数的概率=
| 5 |
| 9 |
∴积为偶数的概率大，所以不同意．
练习册系列答案
相关题目
第一次作横坐标，第二次作纵坐标），指针如果指向分界线上，则重新转动转盘．
