题目内容

仔细观察下列各式，探究规律：12=
1×2×3
6
，12+22=
2×3×5
6
，12+22+32=
3×4×7
6
，…，
（1）根据上述规律，求12+22+32+42+52的值；
（2）你能用一个含有n的算式表示这个规律吗？请写出这个算式；
（3）根据你发现的规律，计算下面算式的值：62+72+82+92+102+112+122+132+142+152．
分析：（1）观察不难发现，从1开始的平方数的和，分母都是6，分子为最后一个数与比它大1的数的积再乘以比这个数的2倍大1的数的积；
（2）根据规律写出即可；
（3）用前15个数的平方和减去前5个数的平方和，列式计算即可得解．
解答：解：（1）12+22+32+42+52=
5×6×11
6
=55；

（2）12+22+32+…+52=
n(n+1)(2n+1)
6
；

（3）62+72+82+92+102+112+122+132+142+152
=（12+22+32+42+52+62+72+82+92+102+112+122+132+142+152）-（12+22+32+42+52）
=
15×16×31
6
-55
=1240-55
=1185．
点评：本题是数字变化规律的考查，难点在于观察出分子的变化情况．
练习册系列答案
相关题目
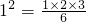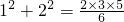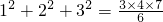观察下列各式：
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，…，…
（1）请根据以上的各式的变形方式，对下列各题进行探究变形：
①
1
2×4
=
1
2
×（
1
2
-
1
4
）
1
2
×（
1
2
-
1
4
）
；②
1
4×6
=
1
2
×（
1
4
-
1
6
）
1
2
×（
1
4
-
1
6
）
；③
1
98×100
=
1
2
×（
1
98
-
1
100
）
1
2
×（
1
98
-
1
100
）
；
（2）由你所找到的规律计算：
1
2×4
+
1
4×6
+
1
6×8
+…+
1
98×100
．
探究：观察下列各式
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，
1
3×4
=
1
3
-
1
4
，…请你根据以上式子的规律填写：
1
1×2
+
1
2×3
+
1
3×4
+
1
4×5
+…+
1
2010×2011
=
2010
2011
2010
2011
；
1
1×3
+
1
3×5
+
1
5×7
…+
1
(2n-1)(2n+1)
=
n
2n+1
n
2n+1
．

仔细观察下列各式，探究规律：数学公式，数学公式，数学公式，…，
（1）根据上述规律，求12+22+32+42+52的值；
（2）你能用一个含有n的算式表示这个规律吗？请写出这个算式；
（3）根据你发现的规律，计算下面算式的值：62+72+82+92+102+112+122+132+142+152．
仔细观察下列各式，探究规律：12=
1×2×3
6
，12+22=
2×3×5
6
，12+22+32=
3×4×7
6
，…，
（1）根据上述规律，求12+22+32+42+52的值；
（2）你能用一个含有n的算式表示这个规律吗？请写出这个算式；
（3）根据你发现的规律，计算下面算式的值：62+72+82+92+102+112+122+132+142+152．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网