题目内容
【题目】如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小
【答案】C
【解析】解:当BD与AC的交点在线段AC上时,如图1所示,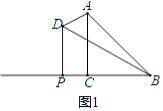
设PC=x,则PD=2x,PB=x+1,
则S△ABD=S梯形ADPC+S△ACB﹣S△PBD= ![]() =
= ![]() ,
,
∴△ABD的面积随x的增大而减小;
当BD与AC的交点在线段CA的延长线上时,如图2所示,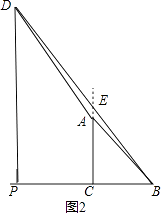
设PC=x,则PD=2x,PB=x+1,
∵△BCE∽△BPD,
∴ ![]() ,
,
即 ![]() ,
,
∴CE= ![]() ,
,
∴AE= ![]() ,
,
∴△ABD的面积是: ![]() =
= ![]() ,
,
∴△ABD的面积随x的增大而增大,
由上可得,△ABD的面积随x的增大先变小后变大,
故选C.
根据题意和函数图象可以得到ABD的面积大小变化情况,从而可以解答本题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目