题目内容
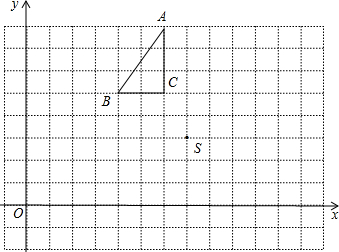 △ABC和点S在平面直角坐标系中的位置如图所示:
△ABC和点S在平面直角坐标系中的位置如图所示:(1)将△ABC向右平移4个单位得到△A1B1C1,则点A1、B1的坐标分别是
(2)将△ABC绕点S按顺时针方向旋转90°,画出旋转后的图形;
(3)求出线段AC在(2)的条件下所扫过的面积.
分析:(1)把A,B两点的横坐标加4,纵坐标不变即可得到平移后的坐标;
(2)以点S为旋转中心,按顺时针方向作∠ASA′=90°,且A′S=AS,得到点A的对应点A′,同法得到其余各点的对应点,顺次连接得到的各点即为旋转后的图形;
(3)线段AC在(2)的条件下所扫过的面积为圆心角为90°,两个半径分别为
和
的扇环的面积.
(2)以点S为旋转中心,按顺时针方向作∠ASA′=90°,且A′S=AS,得到点A的对应点A′,同法得到其余各点的对应点,顺次连接得到的各点即为旋转后的图形;
(3)线段AC在(2)的条件下所扫过的面积为圆心角为90°,两个半径分别为
| 26 |
| 5 |
解答:解:(1)∵点A坐标为(6,8),点B坐标为(4,5),
∴平移后的横坐标加4,纵坐标不变为:A1(10,8)B1(8,5);
(2)
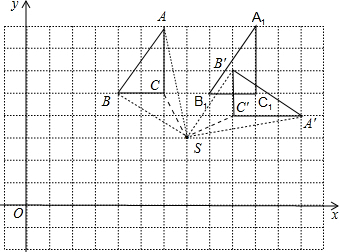
△A′B′C′就是所求的三角形;(图形正确给满分)
(3)∵SC=
=
,SA=
=
,
∴扫过的面积为:
=
.
∴平移后的横坐标加4,纵坐标不变为:A1(10,8)B1(8,5);
(2)

△A′B′C′就是所求的三角形;(图形正确给满分)
(3)∵SC=
| 12+ 22 |
| 5 |
| 52+ 12 |
| 26 |
∴扫过的面积为:
90π×[(
| ||||
| 360 |
| 21π |
| 4 |
点评:求各点的坐标,动手操作画出图形后不易出错;一条线段旋转一定的角度得到的图形的形状是扇环.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 18、△ABC和点S在平面直角坐标系中的位置如图所示:
18、△ABC和点S在平面直角坐标系中的位置如图所示: 22、△ABC和点S在平面直角坐标系中的位置如图所示.
22、△ABC和点S在平面直角坐标系中的位置如图所示. (2012•南宁模拟)△ABC和点S在平面直角坐标系中的位置如图所示:
(2012•南宁模拟)△ABC和点S在平面直角坐标系中的位置如图所示: