题目内容
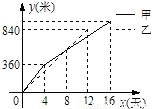
某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队修道路的长度y(米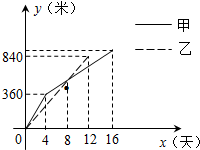 )与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题:
)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题:(1)写出乙工程队修道路的长度y与修筑时间x之间的函数关系式:
(2)甲工程队前4天平均每天修路
(3)该公路的总长度为
分析:(1)设出正比例函数解析式,把(12,840)代入可得所求函数解析式;
(2)让前4天修路的总路程除以4即可得到甲工程队前4天平均每天修路米数,求得甲在第4天到第16天的函数解析式,进而求得后12天修路的总路程,除以12即为后12天平均修路的米数;
(3)让甲修路的总路程+乙修路的总路程即为公路的总长度.
(2)让前4天修路的总路程除以4即可得到甲工程队前4天平均每天修路米数,求得甲在第4天到第16天的函数解析式,进而求得后12天修路的总路程,除以12即为后12天平均修路的米数;
(3)让甲修路的总路程+乙修路的总路程即为公路的总长度.
解答:解:(1)设y=kx,
∵经过(12,840),
∴12k=840,
解得k=70,
∴y=70x,
故答案为y=70x;(2分)
(2)甲工程队前4天平均每天修路米数为360÷4=90;
当x=8时,y=560,
设当4≤x≤16时,甲工程队的函数解析式为y=kx+b,
,
解得
,
∴y=50x+160,
当x=16时,y=960,
∴后12天平均每天修路米数为(960-360)÷12=50.
故答案为90;50(4分)
(3)公路的总长度为840+960=1800米,故答案为1800.(2分)
∵经过(12,840),
∴12k=840,
解得k=70,
∴y=70x,
故答案为y=70x;(2分)
(2)甲工程队前4天平均每天修路米数为360÷4=90;
当x=8时,y=560,
设当4≤x≤16时,甲工程队的函数解析式为y=kx+b,
|
解得
|
∴y=50x+160,
当x=16时,y=960,
∴后12天平均每天修路米数为(960-360)÷12=50.
故答案为90;50(4分)
(3)公路的总长度为840+960=1800米,故答案为1800.(2分)
点评:考查一次函数的应用;数形结合得到所在函数解析式上的点及相关函数解析式是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
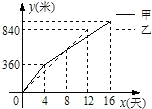 某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.
某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.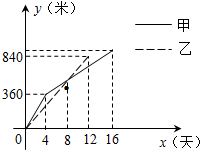 )与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题:
)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,解答下列问题: