题目内容
【题目】如图1，已知l1∥l2 ， 点A，B在直线l1上，点C，D在l2上，连接AD，BC．AE，CE分别是∠BAD，∠BCD的平分线，∠1=70°，∠2=30°．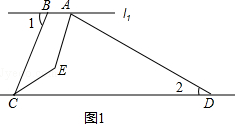 
（1）求∠AEC的度数；
（2）如图2，将线段AD沿线段CD方向平移，其他条件不变，求∠AEC的度数．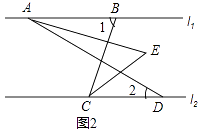 
【答案】
（1）解：如图1，过点E作EF∥l1，
∵l1∥l2，
∴EF∥l2，
∵l1∥l2，
∴∠BCD=∠α，
∵∠1=70°，
∴∠BCD=70°，
∵CE是∠BCD的角平分线，
∴∠ECD= 
×70°=35°，
∵EF∥l2，
∴∠FEC=∠ECD=35°，
∵l1∥l2，
∴∠BAD+∠2=180°，
∵∠2=30°，
∴∠BAD=150°，
∵AE平分∠BAD，
∴∠BAE= ×150°=75°，
∵EF∥l1，
∴∠BAE+∠AEF=180°，
∴∠AEF=105°，
∴∠AEC=105°+35°=140°
（2）解：如图2，过点E作EF∥l1，
∵l1∥l2，
∴EF∥l2，
∵l1∥l2，
∴∠BCD=∠1，
∵∠1=70°，
∴∠BCD=70°，
∵CE是∠BCD的角平分线，
∴∠ECD= ×70°=35°，
∵EF∥l2，
∴∠FEC=∠ECD=35°，
同理可求∠AEF=15°，
∴∠AEC=∠AEF+∠CEF=50°
【解析】（1）利用平行线的性质结合角平分线的性质得出∠BAE以及∠AEF的度数即可得出答案；（2）利用平行线的性质结合角平分线的性质得出∠ECD以及∠AEF的度数即可得出答案．
【考点精析】本题主要考查了平行线的性质和平移的性质的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等才能正确解答此题．
