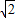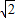题目内容
如果等腰梯形的下底与对角线长都是10厘米,上底与梯形的高相等,则上底的长是( )厘米.
A、5
| ||
B、6
| ||
| C、5 | ||
| D、6 |
分析:根据等腰梯形的性质,作辅助线,利用三角形全等和勾股定理求得上底为6cm.
解答: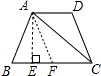 解:如图,已知等腰梯形ABCD,AD=AE,AC=BC=10cm,求AD的长.
解:如图,已知等腰梯形ABCD,AD=AE,AC=BC=10cm,求AD的长.
作AF∥CD
∵AD∥BC
∴四边形AFCD是平行四边形
∴DC=AF,AD=FC
又∵等腰梯形
∴AB=DC=AF
∵AE⊥BF
∴△ABE≌△AFE
∴EF=BE
∴2EF=BC-AD=10-AD
∴在△AEC中:AC2=AD2+(EF+AD)2即:100=AD2+(5+
AD)2∴AD=6或AD=-10(去掉)
∴上底的长为6cm
故选D.
 解:如图,已知等腰梯形ABCD,AD=AE,AC=BC=10cm,求AD的长.
解:如图,已知等腰梯形ABCD,AD=AE,AC=BC=10cm,求AD的长.作AF∥CD
∵AD∥BC
∴四边形AFCD是平行四边形
∴DC=AF,AD=FC
又∵等腰梯形
∴AB=DC=AF
∵AE⊥BF
∴△ABE≌△AFE
∴EF=BE
∴2EF=BC-AD=10-AD
∴在△AEC中:AC2=AD2+(EF+AD)2即:100=AD2+(5+
| 1 |
| 2 |
∴上底的长为6cm
故选D.
点评:本题考查等腰梯形的性质,要求学生能构造直角三角形,借助勾股定理求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目