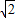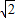Question

如果等腰梯形的下底与对角线长都是10厘米，上底与梯形的高相等，则此梯形的周长是

 

厘米．

Answer 1

分析：画出图形，根据如果等腰梯形的下底与对角线长都是10厘米，上底与梯形的高相等，结合方程可求出解．

解答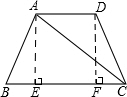：解：作AE⊥BC交BC于E点，DF⊥BC交BC于F点，
设BE=x，则EC=10-x，AE=EF=10-2x，
在Rt△AEC中，AE²+EC²=AC²
（10-2x）²+（10-x）²=10²
x=2或x=10（舍去）．
BE=2，AE=10-2×2=6，
AB=

BE2+AE2

=

22+62

=2

10

．
AD=10-2x=10-2×2=6．
此梯形的周长为：AD+AB+BC+DC=6+2

10

+10+2

10

=16+4

10

．
故答案为：16+4

10

．

点评：本题考查等腰梯形的性质，等腰梯形的腰相等，设出BE的长为x，根据勾股定理求出x，然后求出等腰梯形的各边长，从而求出周长．