题目内容
【题目】如图,数轴上点![]() 、
、![]() 表示的有理数分别为-10、5,点
表示的有理数分别为-10、5,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),点
重合),点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,点
的三等分点,点![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.
的三等分点.
(1)若点![]() 表示的有理数是0,那么
表示的有理数是0,那么![]() 的长为______;若点
的长为______;若点![]() 表示的有理数是1,那么
表示的有理数是1,那么![]() 的长为______.
的长为______.
(2)点![]() 在射线
在射线![]() 上运动(不与点
上运动(不与点![]() 、
、![]() 重合)的过程中,
重合)的过程中,![]() 的长是否发生改变?若不改变,请求出
的长是否发生改变?若不改变,请求出![]() 的长;若改变,请说明理由.
的长;若改变,请说明理由.
【答案】(1)10,10;(2)![]() 的长不会发生改变,且
的长不会发生改变,且![]() .
.
【解析】
(1)由点P表示的有理数为0可得出AP、BP的长度,根据三等分点的定义可得出MP、NP的长度,再由MN=MP+NP即可求出MN的长度;当点P表示的有理数为1时,利用同样的方法求解即可;
(2)设点P表示的有理数是a(a>﹣10且a≠5),分﹣10<a<5及a>5两种情况考虑,由点P表示的有理数可得出AP、BP的长度(用含字母a的代数式表示),根据三等分点的定义可得出MP、NP的长度(用含字母a的代数式表示),再由MN=MP+NP(或MN=MP﹣NP),即可求出MN的长,进而可作出判断.
解:(1)若点P表示的有理数是0,则AP=10,BP=5.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() ,NP=
,NP=![]() BP=
BP=![]() ,
,
∴MN=MP+NP=![]() +
+![]() =10;
=10;
若点P表示的有理数是1,则AP=11,BP=4.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点,
∴MP=![]() AP=
AP=![]() ,NP=
,NP=![]() BP=
BP=![]() ,
,
∴MN=MP+NP=![]() +
+![]() =10.
=10.
故答案为:10,10;
(2)MN的长不会发生改变,理由如下:
设点P表示的有理数是a(a>﹣10且a≠5).
当﹣10<a<5时,如图1,AP=a+10,BP=5﹣a.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+10),NP=
(a+10),NP=![]() BP=
BP=![]() (5﹣a),
(5﹣a),
∴MN=MP+NP=![]() (a+10)+
(a+10)+![]() (5﹣a)=10;
(5﹣a)=10;

当a>5时(如图2),AP=a+10,BP=a﹣5.
∵M是线段AP靠近点A的三等分点,N是线段BP靠近点B的三等分点.
∴MP=![]() AP=
AP=![]() (a+10),NP=
(a+10),NP=![]() BP=
BP=![]() ( a﹣5),
( a﹣5),
∴MN=MP﹣NP=![]() (a+10)-
(a+10)-![]() ( a﹣5)=10.
( a﹣5)=10.
综上所述:点P在射线AB上运动(不与点A,B重合)的过程中,MN的长不会发生变化,且为定值10.


 53随堂测系列答案
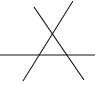
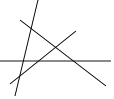
53随堂测系列答案【题目】观察表格:
|
|
| |
1条直线 0个交点 平面分成(1+1)块 | 2条直线 1个交点 平面分成(1+1+2)块 | 3条直线 (1+2)个交点 平面分成(1+1+2+3)块 | 4条直线 (1+2+3)个交点 平面分成(1+1+2+3+4)块 |
根据表格中的规律解答问题:
(1)5条直线两两相交,有 个交点,平面被分成 块;
(2)n条直线两两相交,有 个交点,平面被分成 块;
(3)应用发现的规律解决问题:一张圆饼切10刀(不许重叠),最多可得到 块饼.