Question

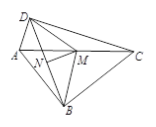
【题目】如图，四边形ABCD中，∠ABC=90°，BD的垂直平分线交AC、BD分别于点M、N，点M为AC中点.

(1) 求证：AM=DM；

(2) 求∠ADC的度数；

(3) 当∠BCD为_______°时，∠BMD为120°．(直接写出结果)

Answer 1

【答案】（1）证明见解析；（2）90°；（3）60

【解析】试题分析：（1）根据“直角三角形斜边上的中线等于斜边的一半”，求出BM，MC的长，然后根据线段垂直平分线的性质得证结论；

（2）根据（1）的结论，然后根据等量代换得到DM=AM=CM，然后根据等边对等角以及三角形的内角和，可得出∠ADC的度数；

（3）根据等边对等角的性质，和三角形的外角性质，可直接根据∠BMD的度数求出∠BCD.

试题解析：(1) ∵∠ABC=90°，点M为AC中点，∴BM=AC，MC=AM=AC，∴AM=BM.∵MN垂直平分BD，∴DM=BM，∴AM=BM；

(2)由(1)知：DM=BM，AM=BM，∴DM=AM.∵MC=AM=AC，∴DM=MC=AM，∴在△ADM中，∠DAM=∠ADM；在△DMC中，∠DCM=∠CDM.∵∠DAM+∠ADM+∠DCM+∠CDM=180°，即：2∠ADM+2∠CDM=180°，∴∠ADM+∠CDM=90°，即∠ADC的度数为90°；

(3)60