题目内容
如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交AC、BC于E、F,且EF=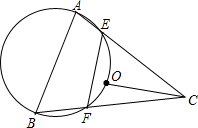 OC,
OC,(1)求证:OC⊥EF;
(2)求:∠AOB的度数.
分析:(1)连接OA,OB,AF,BE,由点O是锐角三角形ABC的外心,又EF=OC,可得OA=OB=EF,即得到它们所对的弧相等,可推出
=
,
=
,所以有∠1=∠3=∠7=∠5,∠2=∠8=∠4=∠6,可证出∠1+∠2=45°.要证OC⊥EF,即证∠1+∠CEF=90°,而∠CEF=∠ABC=∠6+∠7+∠8=∠1+2∠2,因此可得到∠1+∠CEF=2(∠1+∠2)=90°.
(2)利用同弧所对圆心角是它所对的圆周角的2倍即由∠AOB=2∠ACB直接得到.
 |
| AE |
 |
| OF |
 |
| EO |
 |
| BF |
(2)利用同弧所对圆心角是它所对的圆周角的2倍即由∠AOB=2∠ACB直接得到.
解答: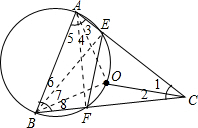 (1)证明:如图,连接OA,OB,AF,BE,
(1)证明:如图,连接OA,OB,AF,BE,
∵点O是锐角三角形ABC的外心,
∴OA=OB=OC,又EF=OC,
∴OA=OB=EF,
∴
=
=
,
∴
=
,
=
∴∠1=∠3=∠7=∠5,∠2=∠8=∠4=∠6
而∠ACB+∠BAC+∠CBA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=4(∠1+∠2)=180°
所以∠1+∠2=45°.
又∠CEF=∠ABC=∠6+∠7+∠8=∠1+2∠2
即∠1+∠CEF=2(∠1+∠2)=90°,
所以OC⊥EF;
(2)解:∠AOB=2(∠1+∠2)=2×45°=90°.
 (1)证明:如图,连接OA,OB,AF,BE,
(1)证明:如图,连接OA,OB,AF,BE,∵点O是锐角三角形ABC的外心,
∴OA=OB=OC,又EF=OC,
∴OA=OB=EF,
∴
 |
| AEO |
 |
| EOF |
 |
| BFO |
∴
 |
| AE |
 |
| OF |
 |
| EO |
 |
| BF |
∴∠1=∠3=∠7=∠5,∠2=∠8=∠4=∠6
而∠ACB+∠BAC+∠CBA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=4(∠1+∠2)=180°
所以∠1+∠2=45°.
又∠CEF=∠ABC=∠6+∠7+∠8=∠1+2∠2
即∠1+∠CEF=2(∠1+∠2)=90°,
所以OC⊥EF;
(2)解:∠AOB=2(∠1+∠2)=2×45°=90°.
点评:本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.同时考查了三角形的外心到三个顶点的距离相等.

练习册系列答案
相关题目
 21、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点(要求画出草图,保留作图痕迹).
21、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点(要求画出草图,保留作图痕迹). 32、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点
32、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点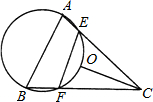 如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.
如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.