题目内容
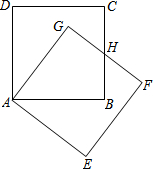 如图所示,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.
如图所示,把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.(1)线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想;
(2)若旋转角为30°,AB=
| 5 |
分析:(1)根据旋转的性质以及HL定理得出Rt△AGH≌Rt△ABH即可得出答案;
(2)利用全等三角形的性质得出∠GAH=∠HAB,GH=BH,进而利用锐角三角函数关系得出HG的长.
(2)利用全等三角形的性质得出∠GAH=∠HAB,GH=BH,进而利用锐角三角函数关系得出HG的长.
解答: 解:(1)HG=HB,
解:(1)HG=HB,
理由:方法1,连结AH,
∵四边形ABCD,AEFG都是正方形
∴∠B=∠G=90°,由题意知AG=AB,
在Rt△AGH和Rt△ABH中
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB;
方法2:连结GB,
∵四边形ABCE,AEFG都是正形,
∴∠ABC=∠AGF=90°
由题意知AB=AG,
∴∠AGB=∠ABG,
∴∠HGB=∠HBG,
∴HG=HB;
(2)∵Rt△AGH≌Rt△ABH,
∴∠GAH=∠HAB,GH=BH,
∵旋转角为30°,AB=
,
∴∠GAH=∠HAB=30°,
∴tan30°=
=
,
∴HG=
×
=
.
 解:(1)HG=HB,
解:(1)HG=HB,理由:方法1,连结AH,
∵四边形ABCD,AEFG都是正方形
∴∠B=∠G=90°,由题意知AG=AB,
在Rt△AGH和Rt△ABH中
|
∴Rt△AGH≌Rt△ABH(HL),
∴HG=HB;
方法2:连结GB,
∵四边形ABCE,AEFG都是正形,
∴∠ABC=∠AGF=90°
由题意知AB=AG,
∴∠AGB=∠ABG,
∴∠HGB=∠HBG,
∴HG=HB;
(2)∵Rt△AGH≌Rt△ABH,
∴∠GAH=∠HAB,GH=BH,
∵旋转角为30°,AB=
| 5 |
∴∠GAH=∠HAB=30°,
∴tan30°=
| HB |
| AB |
| GH |
| AG |
∴HG=
| ||
| 3 |
| 5 |
| ||
| 3 |
点评:此题主要考查了旋转的性质以及锐角三角函数关系以及全等三角形的判定与性质,得出Rt△AGH≌Rt△ABH是解题关键.

练习册系列答案
相关题目
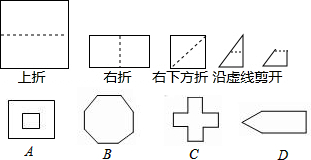
 按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为
按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为 (2010•石家庄模拟)如图所示,每个正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长为( )
(2010•石家庄模拟)如图所示,每个正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方形,那么新正方形的边长为( )