题目内容
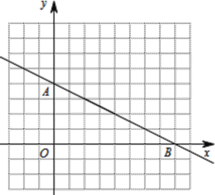
【题目】如图,直线![]() 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为![]() (
(![]() ).
).
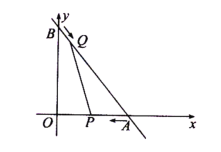
(1)写出A、B两点的坐标;
(2)设![]() 的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,
的面积为S,试求出S与t之间的函数关系式,并求出当t为何值时,![]() 的面积最大;
的面积最大;
(3)当t为何值时,以点A,P,Q为顶点的三角形与![]() 相似?并直接写出此时点Q的坐标.
相似?并直接写出此时点Q的坐标.
【答案】(1)A(6,0),B(0,8);(2)![]() ,当t=3s时,
,当t=3s时,![]() 取得最大值
取得最大值![]() ;(3)当t=
;(3)当t=![]() s时,△APQ与△AOB相似.此时点Q的坐标为(
s时,△APQ与△AOB相似.此时点Q的坐标为(![]() ,
,![]() ).
).
【解析】
(1)分别令y=0,x=0求解即可得到点A、B的坐标
(2)利用勾股定理列式求出AB,然后表示AP、AQ,再利用∠OAB的正弦求出点Q到AP的距离,然后利用三角形的面积列式整理即可
(3)根据相似三角形对应角相等,分∠APQ=90°和∠AQP=90°两种情况,利用∠OAB的余弦列式计算即可得解
解:(1)令y=0,则﹣![]() x+8=0,
x+8=0,
解得x=6,
x=0时,y=8,
∴OA=6,OB=8,
∴点A(6,0),B(0,8);
(2)在Rt△AOB中,由勾股定理得,AB=![]() =
=![]() =10,
=10,
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,
∴AP=2t,
AQ=AB﹣BQ=10﹣t,
∴点Q到AP的距离为AQsin∠OAB=(10﹣t)×![]() =
=![]() (10﹣t),
(10﹣t),
∴△AQP的面积S=![]() ×2t×
×2t×![]() (10﹣t)=﹣
(10﹣t)=﹣![]() (t2﹣10t)=﹣
(t2﹣10t)=﹣![]() (t﹣5)2+20,
(t﹣5)2+20,
∵﹣![]() <0,0<t≤3,
<0,0<t≤3,
∴当t=3时,△AQP的面积最大,S最大=﹣![]() (3﹣5)2+20=
(3﹣5)2+20=![]() ;
;
(3)若∠APQ=90°,则cos∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
若∠AQP=90°,则cos∠OAB=![]() ,
,
∴![]() =
=![]() ,
,
解得t=![]() ,
,
∵0<t≤3,
∴t的值为![]() ,
,
此时,OP=6﹣2×![]() =
=![]() ,
,
PQ=APtan∠OAB=(2×![]() )×
)×![]() =
=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() ),
),
综上所述,t=![]() 秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(
秒时,以点A,P,Q为顶点的三角形与△ABO相似,此时点Q的坐标为(![]() ,
,![]() )
)

 阅读快车系列答案
阅读快车系列答案