Question

问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA。

　 探究∠DBC与∠ABC度数的比值。你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。

　 (1) 当∠BAC=90°时，依问题中的条件补全右图。 观察图形，AB与AC的数量关系为　　 当推出∠DAC=15°时，可进一步推出∠DBC的度数为　　 ；可得到?DBC与∠ABC度数的比值为　　 ；

　 (2) 当∠BAC＝90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与(1)中的结论相同，写出你的猜想并加以证明。

Answer 1

解：(1) 相等；15°；1：3。

(2) 猜想：∠DBC与∠ABC度数的比值与(1)中结论相同。

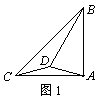
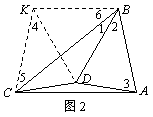
　 证明：如图2，作∠KCA=∠BAC，过B点作BK//AC交CK于点K，

　　　　 连结DK。∵∠BAC¹＝90°，∴四边形ABKC是等腰梯形，

　　　　 ∴CK=AB，∵DC=DA，∴∠DCA=∠DAC，∵∠KCA=∠BAC，

　　　　 ∴∠∴△KCD=∠3，KCD≌△BAD，∴∠2=∠4，KD=BD，

　　　　 ∴KD=BD=BA=KC。∵BK//AC，∴∠ACB=∠6，

　　　　 ∵∠KCA=2∠ACB，∴∠5=∠ACB，∴∠5=∠6，∴KC=KB，

　　　　 ∴KD=BD=KB，∴∠KBD=60°，∵∠ACB=∠6=60°-∠1，

　　　　 ∴∠BAC=2∠ACB=120°-2∠1，

　　　　 ∵∠1+(60°-∠1)+(120°-2∠1)+∠2=180°，∴∠2=2∠1，

　　　　 ∴∠DBC与∠ABC度数的比值为1：3。