题目内容
育红学校七年级学生步行到郊外旅行，七（1）班的学生组成前队，步行速度为4千米/时，七（2）班的学生组成后队，速度为6千米/时，前队出发1小时后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回联络，他骑车的速度为12千米/时，根据上面的事实提出问题并尝试去解答．
问题：
（1）当联络员追上前队时，离出发点多远？
（2）当联络员追上前队再到后队集合，总共用了多少时间？
解：（1）设x小时联络员追上前队，则有方程：4（x+1）=12x，
解得：x=
（小时）．
∴后队走了6×=3千米，前队走了4×+4=6（千米）；
（2）联络员与后队共走（6-3）千米用了t小时
∴t=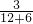
=
（小时）．
所以联络员总共用了30+10=40分钟．
分析：此题是一道开放型题．要注意根据：路程=速度×时间，这一公式提出相关问题．
点评：此题中要注意两队和联络员总是在同时行进，因此要注意行进过程中路程的变化．
（1）当联络员追上前队时，离出发点多远？
（2）当联络员追上前队再到后队集合，总共用了多少时间？
解：（1）设x小时联络员追上前队，则有方程：4（x+1）=12x，
解得：x=
（小时）．∴后队走了6×
=3千米，前队走了4×+4=6（千米）；（2）联络员与后队共走（6-3）千米用了t小时
∴t=
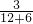=（小时）．所以联络员总共用了30+10=40分钟．
分析：此题是一道开放型题．要注意根据：路程=速度×时间，这一公式提出相关问题．
点评：此题中要注意两队和联络员总是在同时行进，因此要注意行进过程中路程的变化．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目