Question

已知一个等腰梯形的高为2，中位线长为5，一个底角为45°，这个梯形的周长为（　　）

• A、14
• B、15+2

  2

• C、10+2

  2

• D、10+4

  2

Answer 1

分析：根据梯形的中位线定理，可以求得梯形的两底和；只需求得梯形的腰长．
根据等腰直角三角形的性质即可求得等腰梯形的腰长．

解答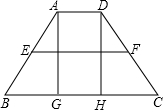：如图，已知：等腰梯形ABCD，高AG、DH=2，中位线EF=5，∠B=45°，求等腰梯形ABCD的周长．
解：在Rt△AGB中，∵AG=2，∠B=45°，∴BG=2，AB=2

2

．
同理可得，CH=2，CD=2

2

．
又∵中位线EF=5，∴

1

2

（AD+BC）=

1

2

（AD+AD+4）=5．
∴AD=3，BC=7．
∴这个梯形的周长=3+7+4

2

=10+4

2

．
故选D．

点评：此题综合性较强，综合利用了等腰直角三角形的性质、勾股定理和梯形的中位线定理．