题目内容
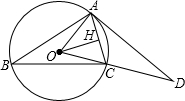 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5| 3 |
(1)∠AOC的度数;
(2)劣弧
 |
| AC |
(3)线段AD的长(结果保留根号).
分析:(1)由圆周角定理得,∠AOC=2∠B=60°;
(2)由等腰三角形的性质:底边上的高与顶角的平分线重合知,∠AOH=30°,故可由余弦的概念求得AO的值,进而由弧长公式求得弧AC的长;
(3)在Rt△AOD中,可由正切的概念求得AD的长.
(2)由等腰三角形的性质:底边上的高与顶角的平分线重合知,∠AOH=30°,故可由余弦的概念求得AO的值,进而由弧长公式求得弧AC的长;
(3)在Rt△AOD中,可由正切的概念求得AD的长.
解答: 解:(1)∠AOC=2∠B=60°.
解:(1)∠AOC=2∠B=60°.
(2)在△AOC中,
∵OH⊥AC,OA=OC,
∴OH是等腰三角形AOC的底边AC上的高,
∴∠AOH=
∠AOC=30°,
∴AO=
=10,
∴
的长=
=
=
,
∴
的长是
.
(3)∵AD是切线,
∴AD⊥OA,
∵∠AOC=60°,
∵tan60°=
,
∴AD=AO•tan60°=10
.
∴线段AD的长是10
.
 解:(1)∠AOC=2∠B=60°.
解:(1)∠AOC=2∠B=60°.(2)在△AOC中,
∵OH⊥AC,OA=OC,
∴OH是等腰三角形AOC的底边AC上的高,
∴∠AOH=
| 1 |
| 2 |
∴AO=
| OH |
| cos30° |
∴
 |
| AC |
| nπr |
| 180 |
| 60×π×10 |
| 180 |
| 10π |
| 3 |
∴
 |
| AC |
| 10π |
| 3 |
(3)∵AD是切线,
∴AD⊥OA,
∵∠AOC=60°,
∵tan60°=
| AD |
| AO |
∴AD=AO•tan60°=10
| 3 |
∴线段AD的长是10
| 3 |
点评:本题利用了圆周角定理,切线的概念,直角三角形和等腰三角形的性质,锐角三角函数的概念,弧长公式求解.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,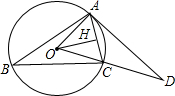
 已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④
已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④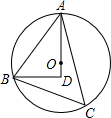 已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=
已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=