题目内容
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5.请求出: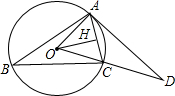
(1)∠AOC的度数;
(2)劣弧AC的长(结果保留π);
(3)线段AD的长(结果保留根号).
分析:(1)直接用圆周角定理得到∠AOC的度数;
(2)由(1)已得到圆心角的度数,再通过特殊角求出半径,最后运用弧长公式求出劣弧AC的长;
(3)由切线的性质可得△OAD是直角三角形,而OA,∠AOC已求,利用特殊角很快就可得到AD的长.
(2)由(1)已得到圆心角的度数,再通过特殊角求出半径,最后运用弧长公式求出劣弧AC的长;
(3)由切线的性质可得△OAD是直角三角形,而OA,∠AOC已求,利用特殊角很快就可得到AD的长.
解答:解:(1)∵∠B=30°,
∴∠AOC=60°(同弧所对的圆心角等于它所对圆周角的2倍);
(2)∵OA=OC,OH⊥AC,
∴∠AOH=
∠AOC=30°,而OH=5,
∴AH=
=
,则OA=
;
∴劣弧AC的长=
=
.
(3)∵AD是⊙O的切线,
∴∠OAD=90°,
又∵∠AOD=60°,OA=
,
∴AD=
OA=10.
∴∠AOC=60°(同弧所对的圆心角等于它所对圆周角的2倍);
(2)∵OA=OC,OH⊥AC,
∴∠AOH=
| 1 |
| 2 |
∴AH=
| 5 | ||
|
5
| ||
| 3 |
10
| ||
| 3 |
∴劣弧AC的长=
60π•
| ||||
| 180 |
10
| ||
| 9 |
(3)∵AD是⊙O的切线,
∴∠OAD=90°,
又∵∠AOD=60°,OA=
10
| ||
| 3 |
∴AD=
| 3 |
点评:本题考查了圆周角定理,垂径定理和切线的性质定理.同时也考查了弧长公式,记住含30度的直角三角形三边的数量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,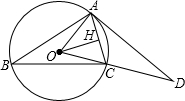 已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=
 已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④
已知:如图△ABC内接于⊙0,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连接BD并延长交EC的延长线于点G,连接AD,分别交CE、BC于点P、Q,下列结论:①∠ABC=∠DBC;②PD=PE:③P是△ACQ的外心;④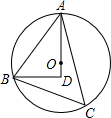 已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=
已知:如图∠ABC内接于⊙O,BD⊥半径OA于D.BD=4.8,sinC=