题目内容
（1）一个多边形的内角和是2340°，求它的边数；
（2）一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？
（2）一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？
考点：多边形内角与外角
专题：计算题
分析：（1）根据多边形的内角和计算公式利用方程作答；
（2）首先计算出每一个外角的度数，再利用外角和除以外角度数可得边数．
（2）首先计算出每一个外角的度数，再利用外角和除以外角度数可得边数．
解答：解：（1）设所求正n边形边数为n，
则（n-2）•180=2340，
解得n=15．
故这个多边形的边数是15；
（2）∵一个多边形的各个内角都相等，且一个内角是150°，
∴外角为30°，
∴边数为360°÷30°=12，
故此多边形是十二边形．
则（n-2）•180=2340，
解得n=15．
故这个多边形的边数是15；
（2）∵一个多边形的各个内角都相等，且一个内角是150°，
∴外角为30°，
∴边数为360°÷30°=12，
故此多边形是十二边形．
点评：此题主要考查了多边形的内角和和外角和计算公式求多边形的边数，解答时要会根据公式进行正确运算．
练习册系列答案
名校课堂系列答案
相关题目
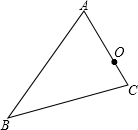画出与△ABC以O为对称中心成中心对称的图形△DEF．
在数轴上分别画出下列各点，A：4.3 B：
如图，在四边形ABCD中，BC＞BA，AD=DC，BD平分∠ABC．
随着车辆的增加，交通违规的现象越来越严重．为了解汽车速度的情况，交警抽取某雷达测速区某时段监测到的200辆汽车的时速（千米/时）进行整理，其中时速大于或等于30千米而小于40千米的汽车有10辆，…，得到其频数及频率如表：