题目内容
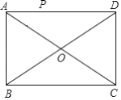
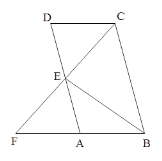
【题目】如图，平行四边形ABCD中，AD=2AB，E为AD的中点，CE的延长线交BA的延长线于点F．
（1）求证：FB=AD．
（2）若∠DAF=70°，求∠EBC的度数．
【答案】（1）详见解析；（2）35°
【解析】
（1）先证明AB=AF，需要找第三个量过渡，由平行四边形的性质可知：AB=CD，再证明AF=CD即可，所以证明△DEC≌△AEF后可得答案； （2）利用平行四边形的性质求
，再证明
可得答案．
证明（1）∵E为AD的中点
∴DE=AE
∵四边形ABCD是平行四边形
∴
，DC=AB
∵
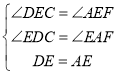
∴△DEC≌△AEF
∴DC=FA
∵AD=2AB
∴AB=DE=EA=FA
∴FB=AD
（2） ∵四边形ABCD是平行四边形，
∴DA∥CB
∴∠CBF=∠DAF= 70°
∴∠AEB=∠EBC
又∵AE=AB
∴∠AEB=∠ABE
∴∠EBC=∠ABE=35°
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
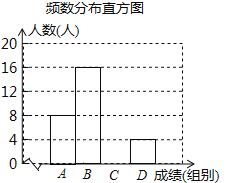
【题目】“品中华诗词，寻文化基因”．某校举办了第二届“中华诗词大赛”，将该校八年级参加竞赛的学生成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图．
频数分布统计表
组别 | 成绩x（分） | 人数 | 百分比 |
A | 60≤x＜70 | 8 | 20% |
B | 70≤x＜80 | 16 | m% |
C | 80≤x＜90 | a | 30% |
D | 90≤＜x≤100 | 4 | 10% |
请观察图表，解答下列问题：
（1）表中a= ，m= ；
（2）补全频数分布直方图；
（3）D组的4名学生中，有1名男生和3名女生．现从中随机抽取2名学生参加市级竞赛，则抽取的2名学生恰好是一名男生和一名女生的概率为 ．
