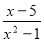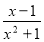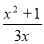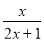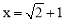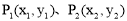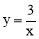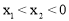题目内容
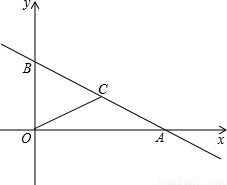
已知：如图，在平面直角坐标系xOy中，直线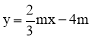
与x轴、y轴分别交于点A、B，点C在线段AB上，且
．
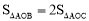（1）求点C的坐标（用含有m的代数式表示）；
（2）将△AOC沿x轴翻折，当点C的对应点C′恰好落在抛物线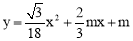
上时，求该抛物线的表达式；
（3）设点M为（2）中所求抛物线上一点，当以A、O、C、M为顶点的四边形为平行四边形时，请直接写出所有满足条件的点M的坐标．
（1）（3，-2m）；（2）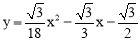
；（3）
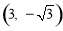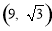或（
或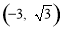
．
【解析】
试题分析：（1）令x=0，即可求得B的纵坐标，令x=0求得x，则A、B的坐标即可求得，根据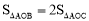
．可以得到C是AB的中点，据此即可求得C的坐标.
（2）求得C关于x轴的对称点，代入抛物线的解析式，即可求得m的值，进而求得抛物线解析式.
（3）分AO是平行四边形的对角线，OC是平行四边形的对角线，AC是平行四边形的对角线三种情况进行讨论，根据平行四边形的对角线互相平分，即可求解．
（1）在直线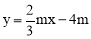
中，令x=0，解得：y=-4m，则B的坐标是（0，-4m），
令y=0，解得：x=6，则A的坐标是（6，0）．
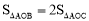∵．∴C是AB的中点.∴C的坐标是（3，-2m）.
（2）∵将△AOC沿x轴翻折，点C的对应点为C′，∴C′的坐标是（3，2m），
代入抛物线的解析式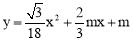
得：
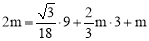，解得：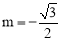
.
∴抛物线的解析式是：.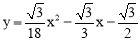
（3）设M的坐标是（x，y），
又C的坐标是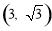
，
当AO是对角线时，AO的中点是（3，0），则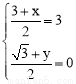
解得：
.
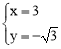则M的坐标是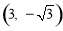，满足函数的解析式.
当AC是平行四边形的对角线时，AC的中点是：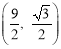
，则M的坐标是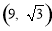是抛物线上的点.
当OC是平行四边形的对角线时，OC的中点是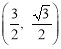
，
则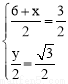
，解得：
.
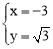则M的坐标是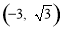．点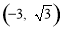是抛物线上的点．
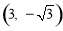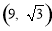综上所述，M的坐标是：或（或．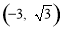
考点：1.一次函数综合题；2.直线上点的坐标与方程的关系；3．翻折对称的性质；4．平行四边形的判定；5.分类思想的应用．
