题目内容
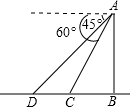 如图,从山顶A处看到地面C点的俯角为60°,看到地面D点的俯角为45°,测得CD=20米,求山AB的高(结果精确到0.1米,参考数据
如图,从山顶A处看到地面C点的俯角为60°,看到地面D点的俯角为45°,测得CD=20米,求山AB的高(结果精确到0.1米,参考数据| 2 |
| 3 |
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造方程关系,进而可求出答案.
解答:解:由已知,可得∠ADB=45°,∠ACB=60°.
∴在Rt△ABD中,DB=AB.
设AB=x,则BD=x,BC=x-20.
∵tan∠ACB=
,
∴AB=CB•tan∠ACB=CB•tan60°.
∴x=
(x-20).
∴x=30+10
.
∴x≈47.3.
答:山AB的高约是47.3米.
∴在Rt△ABD中,DB=AB.
设AB=x,则BD=x,BC=x-20.
∵tan∠ACB=
| AB |
| CB |
∴AB=CB•tan∠ACB=CB•tan60°.
∴x=
| 3 |
∴x=30+10
| 3 |
∴x≈47.3.
答:山AB的高约是47.3米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
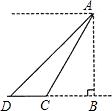 如图,从山顶A处看到地面C点的俯角为60°,看到地面D点的俯角为45°,测得CD=150
如图,从山顶A处看到地面C点的俯角为60°,看到地面D点的俯角为45°,测得CD=150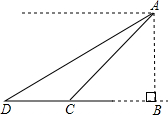 如图,从山顶A处看到地面C点的俯角为45°,看到地面D点的俯角为30°,测得CD=100米,求山高AB的高度.(结果保留根号)
如图,从山顶A处看到地面C点的俯角为45°,看到地面D点的俯角为30°,测得CD=100米,求山高AB的高度.(结果保留根号) 如图,从山顶A处看到地面C点的俯角为45°,看到地面D点的俯角为30°,测得CD=100米,求山高AB的高度.(结果保留根号)
如图,从山顶A处看到地面C点的俯角为45°,看到地面D点的俯角为30°,测得CD=100米,求山高AB的高度.(结果保留根号)