题目内容
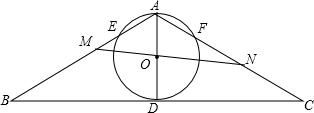 如图,△ABC中,∠B=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AN:NC=2:1,则AM:MB的值为
如图,△ABC中,∠B=∠C=30°,点D是BC边上一点,以AD为直径的⊙O恰与BC边相切,⊙O交AB于E,交AC于F.过O点的直线MN分别交线段BE和CF于M,N,若AN:NC=2:1,则AM:MB的值为
- A.1:2
- B.1:3
- C.2:3
- D.3:5
C
分析:连接OE、OF.设AB=AC=x.根据等腰三角形的性质、切线的性质以及圆的对称性求得AE=OE=AF=OF= AB;然后由平行线的判定与平行线截线段成比例求得ME:AE=3:5,所以BM=AB-AM=
AB;然后由平行线的判定与平行线截线段成比例求得ME:AE=3:5,所以BM=AB-AM= x,据此可以求得AM:MB的值.
x,据此可以求得AM:MB的值.
解答: 连接OE、OF.
连接OE、OF.
∵∠B=∠C=30°,
∴AB=AC(等角对等边);
又∵AD是⊙O的直径,BC边且⊙O于点D,
∴AE=AF(⊙O的对称性),AD⊥BC(切线的性质),
∴∠DAB=∠DAC=60°(等腰三角形的性质);
设AB=AC=x,则AD= AB=
AB= (30°所对的直角边是斜边的一半),
(30°所对的直角边是斜边的一半),
∴AE=OE=AF=OF=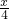 .
.
∵∠DAC=∠EOA=60°,
∴OE∥AC,
∴ME:MA=OE:AN;
∵AN:NC=2:1,
∴AN= x,
x,
∴OE:AN=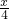 :
: x=3:8,
x=3:8,
∴ME:(AE+EM)=3:8,
∴ME:AE=3:5,
∴AM=AE+ME= x,
x,
∴BM=AB-AM= x,
x,
∴AM:MB=2:3.
故选C.
点评:本题考查了平行线分线段成比例、等腰三角形的判定与性质、切线的性质等知识点.利用平行线分线段成比例定理解题时,要找准对应关系,以免计算错误.
分析:连接OE、OF.设AB=AC=x.根据等腰三角形的性质、切线的性质以及圆的对称性求得AE=OE=AF=OF=
 AB;然后由平行线的判定与平行线截线段成比例求得ME:AE=3:5,所以BM=AB-AM=
AB;然后由平行线的判定与平行线截线段成比例求得ME:AE=3:5,所以BM=AB-AM= x,据此可以求得AM:MB的值.
x,据此可以求得AM:MB的值.解答:
 连接OE、OF.
连接OE、OF.∵∠B=∠C=30°,
∴AB=AC(等角对等边);
又∵AD是⊙O的直径,BC边且⊙O于点D,
∴AE=AF(⊙O的对称性),AD⊥BC(切线的性质),
∴∠DAB=∠DAC=60°(等腰三角形的性质);
设AB=AC=x,则AD=
 AB=
AB= (30°所对的直角边是斜边的一半),
(30°所对的直角边是斜边的一半),∴AE=OE=AF=OF=
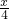 .
. ∵∠DAC=∠EOA=60°,
∴OE∥AC,
∴ME:MA=OE:AN;
∵AN:NC=2:1,
∴AN=
 x,
x,∴OE:AN=
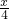 :
: x=3:8,
x=3:8,∴ME:(AE+EM)=3:8,
∴ME:AE=3:5,
∴AM=AE+ME=
 x,
x,∴BM=AB-AM=
 x,
x,∴AM:MB=2:3.
故选C.
点评:本题考查了平行线分线段成比例、等腰三角形的判定与性质、切线的性质等知识点.利用平行线分线段成比例定理解题时,要找准对应关系,以免计算错误.

练习册系列答案
相关题目
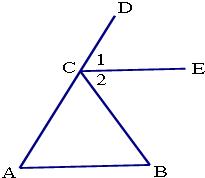 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.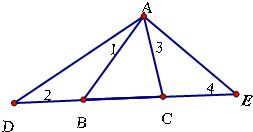 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )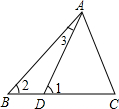 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.