题目内容
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为 . 
【答案】![]() 或10
或10
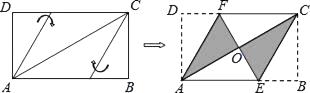
【解析】①如图1,当点F在矩形内部时,
∵四边形ABCD为矩形,AD=5,AB=8,
∴AB=CD,
又∵点F在线段AB的垂直平分线MN上,
∴AN=DM=4,
由折叠性质得:AF=AD=5,DE=FE,
在Rt△ANF中,
∴NF=![]() =3,
=3,
∴FM=5-3=2,
设DE=EF=x,则ME=4-x,
在Rt△ANF中,
∴ME2+MF2=EF2,
即(4-x)2+22=x2,
∴x=![]() .
.
即DE=![]() .
.
②如图2,当点F在矩形外部时,
∵四边形ABCD为矩形,AD=5,AB=8,
∴AB=CD,
又∵点F在线段AB的垂直平分线MN上,
∴AN=DM=4,
由折叠性质得:AF=AD=5,DE=FE,
在Rt△ANF中,
∴NF=![]() =3,
=3,
∴FM=5+3=8,
设DE=EF=y,则ME=y-4,
在Rt△EMF中,
∴ME2+MF2=EF2,
即(y-4)2+82=y2,
∴y=10.
即DE=10.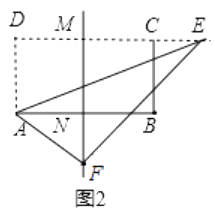
所以答案是:![]() 或10.
或10.
【考点精析】关于本题考查的线段垂直平分线的性质和矩形的性质,需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目