题目内容
如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是( )
| A.9 | B.14 | C. | D. |

D.
解析试题分析:延长DC交l5于点F,延长CD交l1于点E,作点B作BH⊥l1于点H,连接BD,
∵DC⊥l4,l1∥l2∥l3∥l4∥l5,
∴DC⊥l1,DC⊥l5,
∴∠BHA=∠DEA=90°,
∴∠ABH+∠BAH=90°,
∵∠BAD=90°,
∴∠BAH+∠DAE=90°,
∴∠ABH=∠DAE,
∴△BAH∽△ADE,
∴ ,
,
∵AB=3AD,BH=4,DE=1,
∴AE= ,AH=3,
,AH=3,
∴BF=HE=AH+AE=3+ ,
,
在Rt△ADE中,AD= ,
,
∴AB=3AD=5,
∴S四边形ABCD=S△ABD+S△BCD= AB•AD+
AB•AD+ CD•BF=
CD•BF= ×5×
×5× +
+ ×2×
×2×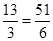 .
.
故选D.
考点:1.相似三角形的判定与性质;2.平行线之间的距离;3.勾股定理.

练习册系列答案
相关题目
下面各图中,∠1与∠2是邻补角的是( )
| A. | B. | C. | D. |
下列四幅图中,∠1和∠2是同位角的是( )
| A.⑴、⑵ | B.⑶、⑷ | C.⑴、⑵、⑶ | D.⑵、⑶、⑷ |
如图, ,
, 平分
平分 ,若
,若 , 则
, 则 的度数是( ).
的度数是( ).
| A.100° | B.110° | C.120° | D.130° |
下例命题不是真命题的是( )
| A.垂直于同一条直线的两直线平行 |
| B.同旁内角互补 |
| C.两点之间,线段最短 |
| D.同角的余角相等 |
以下说法中,正确的个数有( )
(1)直线 外一点与直线上各点连接的所有线段中,垂线段最短;
(2)两条直线被第三条直线所截,内错角相等
(3)经过两点有一条直线,并且只有一条直线
(4)如果一条直线和两条直线中的一条垂直,那么它和另一条直线也垂直
| A.1个 | B.2个 | C.3个 | D.4个 |
如图两平行线a、b被直线l所截,且∠1=60°,则∠2的度数为( )
| A.30 | B.45° | C.60° | D.120° |

