题目内容
如图，在6×6的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点．作△ABC的外接圆⊙O，则 |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：求
的长，关键是求弧所对的圆心角，弧所在圆的半径，连接OC，由图形可知OA⊥OC，即∠AOC=90°，由勾股定理求OA，利用弧长公式求解．
|
| AC |
解答：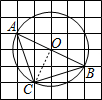
解：连接OC，由图形可知OA⊥OC，
即∠AOC=90°，
由勾股定理，得OA=
=
，
∴
的长=
=
．
故选D．
解：连接OC，由图形可知OA⊥OC，即∠AOC=90°，
由勾股定理，得OA=
| 22+12 |
| 5 |
∴
|
| AC |
90×π×
| ||
| 180 |
| ||
| 2 |
故选D．
点评：本题考查了弧长公式的运用．关键是熟悉公式：扇形的弧长=
．
| n•π•r |
| 180 |
练习册系列答案
相关题目
3、如图，在8×4的方格（每个方格的边长为1个单位长）中，⊙A的半径为1，⊙B的半径为2，将⊙A由图示位置向右平移1个单位长后，⊙A与静止的⊙B的位置关系是（ ）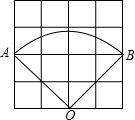
，则扇形OAB周长等于
如图，在8×4的方格（每个方格的边长为1个单位长）中，⊙A的半径为1，⊙B的半径为2，将⊙A由图示位置向右平移几个单位长度后与⊙B内切（ ）
如图，在8×4的方格（每个方格的边长为1个单位长）中，⊙A的半径为l，⊙B的半径为2，将⊙A由图示位置向右平移1个单位长后，⊙A与静止的⊙B的位置关系是（ ）
如图，在10*10的方格纸中，有一个格点四边形ABCD（即四边形的顶点都在格点上），在给出的方格纸上，画出四边形ABCD关于直线L的对称的四边形A1B1C1D1．